improve directory structure
37
beamer/README.org
Normal file
|
|
@ -0,0 +1,37 @@
|
||||||
|
* CCC Beamer Template
|
||||||
|
|
||||||
|
** Install
|
||||||
|
|
||||||
|
To use the template, simply copy all ~*.sty~ files and the ~ccc_img~
|
||||||
|
directory to your project directory.
|
||||||
|
|
||||||
|
You can also install the template in your system, so that you can use it
|
||||||
|
from all your projects. Simply run: ~make install~
|
||||||
|
|
||||||
|
** Usage
|
||||||
|
|
||||||
|
Simply include ~\usetheme{ccc}~ in your document.
|
||||||
|
|
||||||
|
#+BEGIN_SRC latex
|
||||||
|
\documentclass{beamer}
|
||||||
|
\usetheme{ccc}
|
||||||
|
\begin{document}
|
||||||
|
\begin{frame}{This is an Awesome Theme!}
|
||||||
|
\end{frame}
|
||||||
|
\end{document}
|
||||||
|
#+END_SRC
|
||||||
|
|
||||||
|
*** Options
|
||||||
|
- ~cfaedlogo~ places the cfaed logo on every slide
|
||||||
|
- ~noccclogo~ removes the ccc logo from all slides except the title slide
|
||||||
|
|
||||||
|
** Build
|
||||||
|
|
||||||
|
To build the examples, run ~make example~.
|
||||||
|
|
||||||
|
To build your own presentation, please note that this template does not work
|
||||||
|
with ~pdflatex~. Use ~lualatex~ instead! Please contact me, if you need
|
||||||
|
pdflatex support.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
Before 
(image error) Size: 26 KiB After 
(image error) Size: 26 KiB 

|
|
Before 
(image error) Size: 1.5 KiB After 
(image error) Size: 1.5 KiB 

|
|
Before 
(image error) Size: 27 KiB After 
(image error) Size: 27 KiB 

|
|
Before 
(image error) Size: 17 KiB After 
(image error) Size: 17 KiB 

|
|
Before 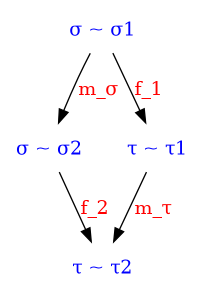
(image error) Size: 9 KiB After 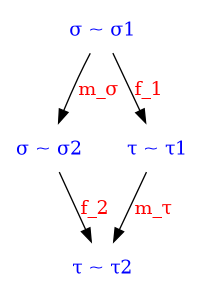
(image error) Size: 9 KiB 

|
BIN
beamer/sea-of-types/target/sea-of-types-0-bytes.png
Normal file
|
After 
(image error) Size: 2.2 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-1-ieee754.png
Normal file
|
After 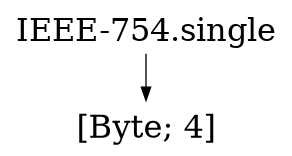
(image error) Size: 6.6 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-10-u8.png
Normal file
|
After 
(image error) Size: 102 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-2-real.png
Normal file
|
After 
(image error) Size: 9.9 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-3-real.png
Normal file
|
After 
(image error) Size: 18 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-4-degrees.png
Normal file
|
After 
(image error) Size: 14 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-5-turns.png
Normal file
|
After 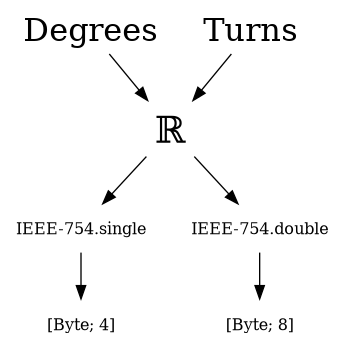
(image error) Size: 16 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-6-radians.png
Normal file
|
After 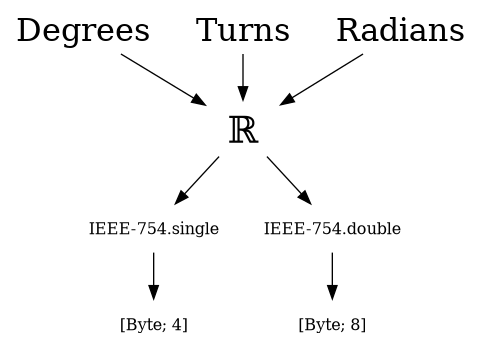
(image error) Size: 21 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-7-angle.png
Normal file
|
After 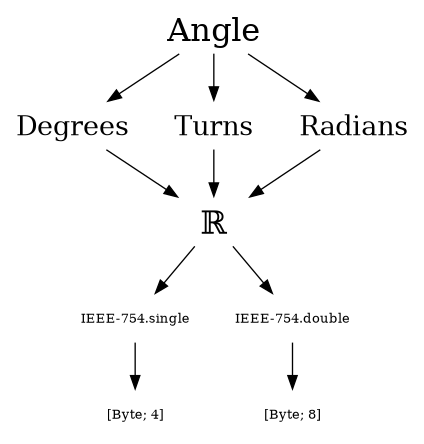
(image error) Size: 22 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-8-hue.png
Normal file
|
After 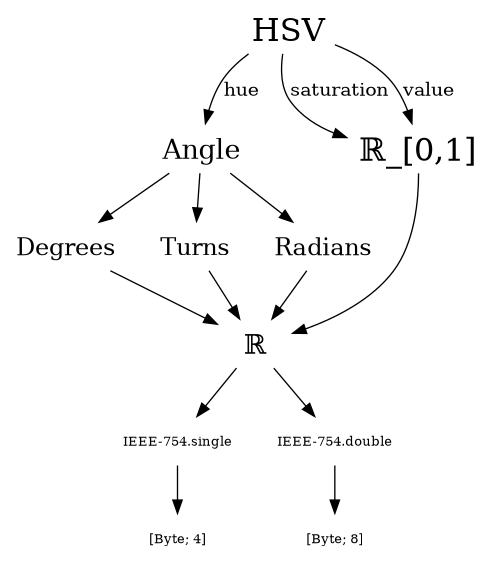
(image error) Size: 34 KiB |
BIN
beamer/sea-of-types/target/sea-of-types-9-u8.png
Normal file
|
After 
(image error) Size: 55 KiB |
|
Before 
(image error) Size: 9.4 KiB After 
(image error) Size: 9.4 KiB 

|
|
Before 
(image error) Size: 8.5 KiB After 
(image error) Size: 8.5 KiB 

|
|
Before 
(image error) Size: 150 KiB After 
(image error) Size: 150 KiB 

|
|
Before 
(image error) Size: 116 KiB After 
(image error) Size: 116 KiB 

|
21
beamer/texput.log
Normal file
|
|
@ -0,0 +1,21 @@
|
||||||
|
This is pdfTeX, Version 3.141592653-2.6-1.40.26 (TeX Live 2024/Arch Linux) (preloaded format=pdflatex 2024.5.29) 23 SEP 2024 17:46
|
||||||
|
entering extended mode
|
||||||
|
\write18 enabled.
|
||||||
|
%&-line parsing enabled.
|
||||||
|
**
|
||||||
|
|
||||||
|
! Emergency stop.
|
||||||
|
<*>
|
||||||
|
|
||||||
|
End of file on the terminal!
|
||||||
|
|
||||||
|
|
||||||
|
Here is how much of TeX's memory you used:
|
||||||
|
3 strings out of 476023
|
||||||
|
111 string characters out of 5791582
|
||||||
|
1925187 words of memory out of 5000000
|
||||||
|
22228 multiletter control sequences out of 15000+600000
|
||||||
|
558069 words of font info for 36 fonts, out of 8000000 for 9000
|
||||||
|
14 hyphenation exceptions out of 8191
|
||||||
|
0i,0n,0p,1b,6s stack positions out of 10000i,1000n,20000p,200000b,200000s
|
||||||
|
! ==> Fatal error occurred, no output PDF file produced!
|
||||||
41
share/cc-beamer-template-master/Makefile
Normal file
|
|
@ -0,0 +1,41 @@
|
||||||
|
PACKAGE_STY = $(wildcard *.sty)
|
||||||
|
PACKAGE_IMG = $(wildcard ccc_img/*)
|
||||||
|
|
||||||
|
DESTDIR ?= $(shell kpsewhich -var-value=TEXMFHOME)
|
||||||
|
INSTALL_DIR = $(DESTDIR)/tex/latex/ccc
|
||||||
|
|
||||||
|
EXAMPLE_SRC = example.tex
|
||||||
|
EXAMPLE_PDF = example.pdf
|
||||||
|
|
||||||
|
CACHE_DIR := $(shell pwd)/.latex-cache
|
||||||
|
|
||||||
|
COMPILE_TEX := latexmk -lualatex -output-directory="$(CACHE_DIR)"
|
||||||
|
|
||||||
|
.PHONY: install uninstall example all clean
|
||||||
|
|
||||||
|
all: example
|
||||||
|
|
||||||
|
example: $(EXAMPLE_PDF)
|
||||||
|
|
||||||
|
install: $(PACKAGE_STY)
|
||||||
|
@mkdir -p "$(INSTALL_DIR)"
|
||||||
|
@cp $(PACKAGE_STY) "$(INSTALL_DIR)"
|
||||||
|
@mkdir -p "$(INSTALL_DIR)/ccc_img"
|
||||||
|
@cp $(PACKAGE_IMG) "$(INSTALL_DIR)/ccc_img"
|
||||||
|
|
||||||
|
uninstall:
|
||||||
|
@rm -f $(addprefix "$(INSTALL_DIR)"/, $(PACKAGE_STY))
|
||||||
|
@rm -f $(addprefix "$(INSTALL_DIR)"/, $(PACKAGE_IMG))
|
||||||
|
@rmdir "$(INSTALL_DIR)/ccc_img"
|
||||||
|
@rmdir "$(INSTALL_DIR)"
|
||||||
|
|
||||||
|
clean:
|
||||||
|
@rm -rf "$(CACHE_DIR)"
|
||||||
|
@rm -f "$(EXAMPLE_PDF)"
|
||||||
|
|
||||||
|
$(EXAMPLE_PDF) : $(EXAMPLE_SRC)
|
||||||
|
@$(COMPILE_TEX) $(EXAMPLE_SRC)
|
||||||
|
@cp "$(CACHE_DIR)/$(EXAMPLE_PDF)" .
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
37
share/cc-beamer-template-master/README.org
Normal file
|
|
@ -0,0 +1,37 @@
|
||||||
|
* CCC Beamer Template
|
||||||
|
|
||||||
|
** Install
|
||||||
|
|
||||||
|
To use the template, simply copy all ~*.sty~ files and the ~ccc_img~
|
||||||
|
directory to your project directory.
|
||||||
|
|
||||||
|
You can also install the template in your system, so that you can use it
|
||||||
|
from all your projects. Simply run: ~make install~
|
||||||
|
|
||||||
|
** Usage
|
||||||
|
|
||||||
|
Simply include ~\usetheme{ccc}~ in your document.
|
||||||
|
|
||||||
|
#+BEGIN_SRC latex
|
||||||
|
\documentclass{beamer}
|
||||||
|
\usetheme{ccc}
|
||||||
|
\begin{document}
|
||||||
|
\begin{frame}{This is an Awesome Theme!}
|
||||||
|
\end{frame}
|
||||||
|
\end{document}
|
||||||
|
#+END_SRC
|
||||||
|
|
||||||
|
*** Options
|
||||||
|
- ~cfaedlogo~ places the cfaed logo on every slide
|
||||||
|
- ~noccclogo~ removes the ccc logo from all slides except the title slide
|
||||||
|
|
||||||
|
** Build
|
||||||
|
|
||||||
|
To build the examples, run ~make example~.
|
||||||
|
|
||||||
|
To build your own presentation, please note that this template does not work
|
||||||
|
with ~pdflatex~. Use ~lualatex~ instead! Please contact me, if you need
|
||||||
|
pdflatex support.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
31
share/cc-beamer-template-master/beamercolorthemeccc.sty
Normal file
|
|
@ -0,0 +1,31 @@
|
||||||
|
\mode<presentation>
|
||||||
|
|
||||||
|
\definecolor{darkblue}{HTML}{265E87}
|
||||||
|
\definecolor{darkteal}{RGB}{0,180,141}
|
||||||
|
\definecolor{orange}{RGB}{231,123,20}
|
||||||
|
\definecolor{gray}{rgb}{0.929,0.929,0.929}
|
||||||
|
|
||||||
|
% Settings
|
||||||
|
\setbeamercolor*{title page header}{fg=darkblue}
|
||||||
|
\setbeamercolor*{author}{fg=darkblue}
|
||||||
|
\setbeamercolor*{institute}{fg=darkblue}
|
||||||
|
\setbeamercolor*{date}{fg=darkblue}
|
||||||
|
\setbeamercolor*{frametitle}{fg=darkblue}
|
||||||
|
\setbeamercolor*{framesubtitle}{fg=darkblue}
|
||||||
|
\setbeamercolor*{pagenum}{fg=darkblue}
|
||||||
|
\setbeamercolor*{alerted text}{fg=orange}
|
||||||
|
\setbeamercolor*{item}{fg=darkblue}
|
||||||
|
\setbeamercolor*{subitem}{fg=darkteal}
|
||||||
|
\setbeamercolor*{subsubitem}{fg=orange}
|
||||||
|
\setbeamercolor*{block title}{fg=darkblue}
|
||||||
|
\setbeamercolor*{block title alerted}{fg=orange}
|
||||||
|
\setbeamercolor*{block title example}{fg=darkteal}
|
||||||
|
\setbeamercolor*{block body}{fg=black}
|
||||||
|
\setbeamercolor*{bibliography entry title}{fg=black}
|
||||||
|
\setbeamercolor*{bibliography entry author}{fg=darkblue}
|
||||||
|
\setbeamercolor*{bibliography entry location}{fg=black}
|
||||||
|
\setbeamercolor*{bibliography entry note}{fg=black}
|
||||||
|
\setbeamercolor*{section in toc}{fg=darkblue}
|
||||||
|
\setbeamercolor*{subsection in toc}{fg=darkteal}
|
||||||
|
|
||||||
|
\mode<all>
|
||||||
11
share/cc-beamer-template-master/beamerfontthemeccc.sty
Normal file
|
|
@ -0,0 +1,11 @@
|
||||||
|
\mode<presentation>
|
||||||
|
|
||||||
|
\setbeamerfont{title}{size=\Large,series=\bfseries}
|
||||||
|
\setbeamerfont{subtitle}{series=\bfseries}
|
||||||
|
\setbeamerfont{frametitle}{size=\large, series=\bfseries}
|
||||||
|
\setbeamerfont{framesubtitle}{size=\small, series=\bfseries}
|
||||||
|
\setbeamerfont{pagenum}{size=\footnotesize}
|
||||||
|
\setbeamerfont{block body}{size=\normalsize}
|
||||||
|
\setbeamerfont{footnote}{size=\scriptsize}
|
||||||
|
|
||||||
|
\mode<all>
|
||||||
182
share/cc-beamer-template-master/beamerinnerthemeccc.sty
Normal file
|
|
@ -0,0 +1,182 @@
|
||||||
|
\mode<presentation>
|
||||||
|
|
||||||
|
\def\beamer@andinst{\\[0.5em]}
|
||||||
|
|
||||||
|
\setbeamertemplate{background}{
|
||||||
|
\begin{tikzpicture}
|
||||||
|
\useasboundingbox (0,0) rectangle(\the\paperwidth,\the\paperheight);
|
||||||
|
% the header
|
||||||
|
\fill[gray, anchor=north west] (0,\the\paperheight) rectangle(\the\paperwidth,\paperheight-1.4cm);
|
||||||
|
% ccc logo on the left (only on title page)
|
||||||
|
\ifnum\thepage=1\relax%
|
||||||
|
\node[anchor=west, inner sep=0] (header) at (0.25cm,\paperheight-0.7cm) {
|
||||||
|
\includegraphics[width=90px]{ccc_img/cclogo.pdf}};
|
||||||
|
\fi
|
||||||
|
% cfaed logo on the right (only on title page or if cfaedlogo is set)
|
||||||
|
\ifbeamer@cfaedlogo
|
||||||
|
\node[anchor=east, inner sep=0] (header) at (\paperwidth-0.25cm,\paperheight-0.7cm) {
|
||||||
|
\includegraphics[width=60px]{ccc_img/cfaed.png}};
|
||||||
|
\else
|
||||||
|
\ifnum\thepage=1\relax%
|
||||||
|
\node[anchor=east, inner sep=0] (header) at (\paperwidth-0.25cm,\paperheight-0.7cm) {
|
||||||
|
\includegraphics[width=60px]{ccc_img/cfaed.png}};
|
||||||
|
\fi
|
||||||
|
\fi
|
||||||
|
% the footer
|
||||||
|
\node[anchor=south west, inner sep=0] (footer) at (0,0) {
|
||||||
|
\ifnum\thepage=1\relax%
|
||||||
|
\includegraphics[width=\paperwidth]{ccc_img/titlefooter.png}
|
||||||
|
\fi
|
||||||
|
\includegraphics[width=\paperwidth]{ccc_img/footer.png}};
|
||||||
|
\ifnum\thepage>1\relax%
|
||||||
|
% page number on the left
|
||||||
|
\node[anchor=west, inner sep=0] (pagenum) at (0.2,0.55) {
|
||||||
|
\usebeamerfont{pagenum}\usebeamercolor[fg]{pagenum}\insertframenumber};
|
||||||
|
% page ccc logo on the right
|
||||||
|
\ifbeamer@ccclogo
|
||||||
|
\node[anchor=east, inner sep=0] (pagenum) at (\pagewidth-0.2,0.55) {
|
||||||
|
\includegraphics[width=50pt]{ccc_img/cclogo.pdf}};
|
||||||
|
\fi
|
||||||
|
\fi
|
||||||
|
\end{tikzpicture}
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{title page}{ccc}[1][]{
|
||||||
|
\vskip1cm%
|
||||||
|
\begin{beamercolorbox}[wd=\textwidth,#1]{title page header}
|
||||||
|
\usebeamerfont{title}\inserttitle\par%
|
||||||
|
\medskip
|
||||||
|
\usebeamerfont{subtitle}\insertsubtitle\par%
|
||||||
|
\end{beamercolorbox}%
|
||||||
|
\vskip0.5cm%
|
||||||
|
\begin{beamercolorbox}[wd=\textwidth,#1]{author}
|
||||||
|
\usebeamerfont{author}\insertauthor%
|
||||||
|
\end{beamercolorbox}
|
||||||
|
\vskip0.5cm%
|
||||||
|
\begin{beamercolorbox}[wd=\textwidth,#1]{institute}
|
||||||
|
\usebeamerfont{institute}\insertinstitute%
|
||||||
|
\end{beamercolorbox}
|
||||||
|
\vskip0.5cm%
|
||||||
|
\begin{beamercolorbox}[wd=\textwidth,#1]{date}
|
||||||
|
\usebeamerfont{date}\insertdate%
|
||||||
|
\end{beamercolorbox}
|
||||||
|
\vfill
|
||||||
|
}
|
||||||
|
|
||||||
|
% Frame title
|
||||||
|
\defbeamertemplate*{frametitle}{ccc}[1][]
|
||||||
|
{
|
||||||
|
\begin{tikzpicture}
|
||||||
|
\useasboundingbox (0,0) rectangle(\textwidth,1.4cm);
|
||||||
|
\ifx\insertframesubtitle\@empty%
|
||||||
|
\node[anchor=west, inner sep=0, text width=\textwidth, align=left] at (0,0.7){
|
||||||
|
\usebeamerfont{frametitle}\insertframetitle};
|
||||||
|
\else
|
||||||
|
\node[anchor=west, inner sep=0, text width=\textwidth, align=left] at (0,0.7){
|
||||||
|
\usebeamerfont{frametitle}\insertframetitle\\
|
||||||
|
\usebeamerfont{framesubtitle}\insertframesubtitle};
|
||||||
|
\fi
|
||||||
|
\end{tikzpicture}
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{block begin}{ccc}
|
||||||
|
{
|
||||||
|
\par\vskip\medskipamount%
|
||||||
|
\usebeamercolor{block title}
|
||||||
|
\begin{tikzpicture}
|
||||||
|
\node [
|
||||||
|
draw=fg, inner sep=1ex,
|
||||||
|
text width=\textwidth-2ex-1pt,
|
||||||
|
minimum width=\textwidth-1pt,
|
||||||
|
rounded corners
|
||||||
|
] (BOXCONTENT) \bgroup%
|
||||||
|
\ifx\insertblocktitle\@empty\else\par\fi
|
||||||
|
\usebeamerfont{block body}
|
||||||
|
\usebeamercolor[fg]{block body}
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{block end}{ccc}
|
||||||
|
{
|
||||||
|
\egroup;
|
||||||
|
\usebeamercolor{block title}
|
||||||
|
\ifx\insertblocktitle\@empty
|
||||||
|
\else{
|
||||||
|
\node[ fill=bg, anchor=west, text=fg, rounded corners ] at
|
||||||
|
([shift={(5pt,0)}]BOXCONTENT.north west) {\insertblocktitle};
|
||||||
|
}
|
||||||
|
\fi
|
||||||
|
\end{tikzpicture}
|
||||||
|
\vskip\smallskipamount
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{block example begin}{ccc}
|
||||||
|
{
|
||||||
|
\par\vskip\medskipamount%
|
||||||
|
\usebeamercolor{block title example}
|
||||||
|
\begin{tikzpicture}
|
||||||
|
\node [
|
||||||
|
draw=fg, inner sep=1ex,
|
||||||
|
text width=\textwidth-2ex-1pt,
|
||||||
|
minimum width=\textwidth-1pt,
|
||||||
|
rounded corners
|
||||||
|
] (BOXCONTENT) \bgroup%
|
||||||
|
\ifx\insertblocktitle\@empty\else\par\fi
|
||||||
|
\usebeamerfont{block body}
|
||||||
|
\usebeamercolor[fg]{block body}
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{block example end}{ccc}
|
||||||
|
{
|
||||||
|
\egroup;
|
||||||
|
\usebeamercolor{block title example}
|
||||||
|
\ifx\insertblocktitle\@empty
|
||||||
|
\else%
|
||||||
|
{
|
||||||
|
\node [ fill=bg, anchor=west, text=fg, rounded corners]
|
||||||
|
at ([shift={(5pt,0)}]BOXCONTENT.north west) {\insertblocktitle};
|
||||||
|
}
|
||||||
|
\fi
|
||||||
|
\end{tikzpicture}
|
||||||
|
\vskip\smallskipamount
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{block alerted begin}{ccc}
|
||||||
|
{
|
||||||
|
\par\vskip\medskipamount%
|
||||||
|
\usebeamercolor{block title alerted}
|
||||||
|
\begin{tikzpicture}
|
||||||
|
\node [
|
||||||
|
draw=fg, inner sep=1ex,
|
||||||
|
text width=\textwidth-2ex-1pt,
|
||||||
|
minimum width=\textwidth-1pt,
|
||||||
|
rounded corners
|
||||||
|
] (BOXCONTENT) \bgroup%
|
||||||
|
\ifx\insertblocktitle\@empty\else\par\fi
|
||||||
|
\usebeamerfont{block body}
|
||||||
|
\usebeamercolor[fg]{block body}
|
||||||
|
}
|
||||||
|
|
||||||
|
\defbeamertemplate*{block alerted end}{ccc}
|
||||||
|
{
|
||||||
|
\egroup;
|
||||||
|
\usebeamercolor{block title alerted}
|
||||||
|
\ifx\insertblocktitle\@empty
|
||||||
|
\else%
|
||||||
|
{
|
||||||
|
\node [fill=bg, anchor=west, text=fg, rounded corners] at
|
||||||
|
([shift={(5pt,0)}]BOXCONTENT.north west) {\insertblocktitle};
|
||||||
|
}
|
||||||
|
\fi
|
||||||
|
\end{tikzpicture}
|
||||||
|
\vskip\smallskipamount
|
||||||
|
}
|
||||||
|
|
||||||
|
% Items
|
||||||
|
\setbeamertemplate{itemize items}{\Squarepipe}
|
||||||
|
|
||||||
|
\setbeamertemplate{footline}{\vspace{4mm}}
|
||||||
|
|
||||||
|
\setbeamertemplate{section in toc}[sections numbered]
|
||||||
|
\setbeamertemplate{subsection in toc}[subsections numbered]
|
||||||
|
|
||||||
|
\mode<all>
|
||||||
0
share/cc-beamer-template-master/beamerouterthemeccc.sty
Normal file
31
share/cc-beamer-template-master/beamerthemeccc.sty
Normal file
|
|
@ -0,0 +1,31 @@
|
||||||
|
\newif\ifbeamer@cfaedlogo
|
||||||
|
\beamer@cfaedlogofalse
|
||||||
|
\DeclareOptionBeamer{cfaedlogo}{\beamer@cfaedlogotrue}
|
||||||
|
\ProcessOptionsBeamer
|
||||||
|
|
||||||
|
\newif\ifbeamer@ccclogo
|
||||||
|
\beamer@ccclogotrue
|
||||||
|
\DeclareOptionBeamer{noccclogo}{\beamer@ccclogofalse}
|
||||||
|
\ProcessOptionsBeamer
|
||||||
|
|
||||||
|
\mode<presentation>
|
||||||
|
|
||||||
|
% Requirement
|
||||||
|
\RequirePackage{tikz}
|
||||||
|
\usetikzlibrary{calc}
|
||||||
|
\RequirePackage{fontspec}
|
||||||
|
\RequirePackage{marvosym}
|
||||||
|
|
||||||
|
% Settings
|
||||||
|
\useinnertheme{ccc}
|
||||||
|
\useoutertheme{ccc}
|
||||||
|
\usecolortheme{ccc}
|
||||||
|
\usefonttheme{ccc}
|
||||||
|
|
||||||
|
% Set the font
|
||||||
|
\setsansfont{Open Sans}
|
||||||
|
|
||||||
|
% disable navigation symbols
|
||||||
|
\setbeamertemplate{navigation symbols}{}
|
||||||
|
|
||||||
|
\mode<all>
|
||||||
BIN
share/cc-beamer-template-master/ccc_img/cfaed.png
Executable file
|
After 
(image error) Size: 26 KiB |
BIN
share/cc-beamer-template-master/ccc_img/footer.png
Executable file
|
After 
(image error) Size: 1.5 KiB |
BIN
share/cc-beamer-template-master/ccc_img/header.png
Executable file
|
After 
(image error) Size: 27 KiB |
BIN
share/cc-beamer-template-master/ccc_img/titlefooter.png
Normal file
|
After 
(image error) Size: 17 KiB |
64
share/cc-beamer-template-master/example.tex
Normal file
|
|
@ -0,0 +1,64 @@
|
||||||
|
\documentclass{beamer}
|
||||||
|
|
||||||
|
\title{There Is No Largest Prime Number}
|
||||||
|
\date[ISPN ’80]{27th International Symposium of Prime Numbers}
|
||||||
|
\author[Euclid]{Euclid of Alexandria \texttt{euclid@alexandria.edu}\inst{1}}
|
||||||
|
\institute{\inst{1} University of Alexandria}
|
||||||
|
|
||||||
|
\usetheme{ccc}
|
||||||
|
|
||||||
|
\begin{document}
|
||||||
|
|
||||||
|
\begin{frame}
|
||||||
|
\titlepage
|
||||||
|
\end{frame}
|
||||||
|
|
||||||
|
\begin{frame}
|
||||||
|
\frametitle{There Is No Largest Prime Number}
|
||||||
|
\framesubtitle{The proof uses \textit{reductio ad absurdum}.}
|
||||||
|
\begin{theorem}
|
||||||
|
There is no largest prime number.
|
||||||
|
\end{theorem}
|
||||||
|
\begin{enumerate}
|
||||||
|
\item<1-| alert@1> Suppose $p$ were the largest prime number.
|
||||||
|
\item<2-> Let $q$ be the product of the first $p$ numbers.
|
||||||
|
\item<3-> Then $q+1$ is not divisible by any of them.
|
||||||
|
\item<1-> But $q + 1$ is greater than $1$, thus divisible by some prime
|
||||||
|
number not in the first $p$ numbers.
|
||||||
|
\end{enumerate}
|
||||||
|
\end{frame}
|
||||||
|
|
||||||
|
\begin{frame}{Itemize and Enumerations}
|
||||||
|
\begin{itemize}
|
||||||
|
\item one
|
||||||
|
\item two
|
||||||
|
\item three
|
||||||
|
\begin{enumerate}
|
||||||
|
\item one
|
||||||
|
\item two
|
||||||
|
\item three
|
||||||
|
\begin{itemize}
|
||||||
|
\item one
|
||||||
|
\item two
|
||||||
|
\item three
|
||||||
|
\end{itemize}
|
||||||
|
\end{enumerate}
|
||||||
|
\end{itemize}
|
||||||
|
\end{frame}
|
||||||
|
|
||||||
|
\begin{frame}{Playing with blocks}
|
||||||
|
\begin{block}{}
|
||||||
|
Just a block.
|
||||||
|
\end{block}
|
||||||
|
\begin{block}{A Block}
|
||||||
|
Another block with a title and some very long text. This text is so long
|
||||||
|
that it goes about multiple lines. \\
|
||||||
|
It is also important to \\
|
||||||
|
have line breaks working!
|
||||||
|
\end{block}
|
||||||
|
\begin{example}
|
||||||
|
Something useful could be written here.
|
||||||
|
\end{example}
|
||||||
|
\end{frame}
|
||||||
|
|
||||||
|
\end{document}
|
||||||
36
share/popl08-tutorial-Fsub/.Makefile.d
Normal file
|
|
@ -0,0 +1,36 @@
|
||||||
|
AdditionalTactics.vo AdditionalTactics.glob AdditionalTactics.v.beautified AdditionalTactics.required_vo: AdditionalTactics.v
|
||||||
|
AdditionalTactics.vio: AdditionalTactics.v
|
||||||
|
AdditionalTactics.vos AdditionalTactics.vok AdditionalTactics.required_vos: AdditionalTactics.v
|
||||||
|
FSetDecide.vo FSetDecide.glob FSetDecide.v.beautified FSetDecide.required_vo: FSetDecide.v
|
||||||
|
FSetDecide.vio: FSetDecide.v
|
||||||
|
FSetDecide.vos FSetDecide.vok FSetDecide.required_vos: FSetDecide.v
|
||||||
|
FSetNotin.vo FSetNotin.glob FSetNotin.v.beautified FSetNotin.required_vo: FSetNotin.v AdditionalTactics.vo
|
||||||
|
FSetNotin.vio: FSetNotin.v AdditionalTactics.vio
|
||||||
|
FSetNotin.vos FSetNotin.vok FSetNotin.required_vos: FSetNotin.v AdditionalTactics.vos
|
||||||
|
ListFacts.vo ListFacts.glob ListFacts.v.beautified ListFacts.required_vo: ListFacts.v AdditionalTactics.vo
|
||||||
|
ListFacts.vio: ListFacts.v AdditionalTactics.vio
|
||||||
|
ListFacts.vos ListFacts.vok ListFacts.required_vos: ListFacts.v AdditionalTactics.vos
|
||||||
|
FiniteSets.vo FiniteSets.glob FiniteSets.v.beautified FiniteSets.required_vo: FiniteSets.v ListFacts.vo AdditionalTactics.vo
|
||||||
|
FiniteSets.vio: FiniteSets.v ListFacts.vio AdditionalTactics.vio
|
||||||
|
FiniteSets.vos FiniteSets.vok FiniteSets.required_vos: FiniteSets.v ListFacts.vos AdditionalTactics.vos
|
||||||
|
Atom.vo Atom.glob Atom.v.beautified Atom.required_vo: Atom.v FiniteSets.vo FSetDecide.vo FSetNotin.vo ListFacts.vo AdditionalTactics.vo
|
||||||
|
Atom.vio: Atom.v FiniteSets.vio FSetDecide.vio FSetNotin.vio ListFacts.vio AdditionalTactics.vio
|
||||||
|
Atom.vos Atom.vok Atom.required_vos: Atom.v FiniteSets.vos FSetDecide.vos FSetNotin.vos ListFacts.vos AdditionalTactics.vos
|
||||||
|
Metatheory.vo Metatheory.glob Metatheory.v.beautified Metatheory.required_vo: Metatheory.v AdditionalTactics.vo Atom.vo Environment.vo
|
||||||
|
Metatheory.vio: Metatheory.v AdditionalTactics.vio Atom.vio Environment.vio
|
||||||
|
Metatheory.vos Metatheory.vok Metatheory.required_vos: Metatheory.v AdditionalTactics.vos Atom.vos Environment.vos
|
||||||
|
Environment.vo Environment.glob Environment.v.beautified Environment.required_vo: Environment.v ListFacts.vo Atom.vo
|
||||||
|
Environment.vio: Environment.v ListFacts.vio Atom.vio
|
||||||
|
Environment.vos Environment.vok Environment.required_vos: Environment.v ListFacts.vos Atom.vos
|
||||||
|
Fsub_Definitions.vo Fsub_Definitions.glob Fsub_Definitions.v.beautified Fsub_Definitions.required_vo: Fsub_Definitions.v Metatheory.vo
|
||||||
|
Fsub_Definitions.vio: Fsub_Definitions.v Metatheory.vio
|
||||||
|
Fsub_Definitions.vos Fsub_Definitions.vok Fsub_Definitions.required_vos: Fsub_Definitions.v Metatheory.vos
|
||||||
|
Fsub_Infrastructure.vo Fsub_Infrastructure.glob Fsub_Infrastructure.v.beautified Fsub_Infrastructure.required_vo: Fsub_Infrastructure.v Fsub_Definitions.vo
|
||||||
|
Fsub_Infrastructure.vio: Fsub_Infrastructure.v Fsub_Definitions.vio
|
||||||
|
Fsub_Infrastructure.vos Fsub_Infrastructure.vok Fsub_Infrastructure.required_vos: Fsub_Infrastructure.v Fsub_Definitions.vos
|
||||||
|
Fsub_Lemmas.vo Fsub_Lemmas.glob Fsub_Lemmas.v.beautified Fsub_Lemmas.required_vo: Fsub_Lemmas.v Fsub_Infrastructure.vo AdditionalTactics.vo
|
||||||
|
Fsub_Lemmas.vio: Fsub_Lemmas.v Fsub_Infrastructure.vio AdditionalTactics.vio
|
||||||
|
Fsub_Lemmas.vos Fsub_Lemmas.vok Fsub_Lemmas.required_vos: Fsub_Lemmas.v Fsub_Infrastructure.vos AdditionalTactics.vos
|
||||||
|
Fsub_Soundness.vo Fsub_Soundness.glob Fsub_Soundness.v.beautified Fsub_Soundness.required_vo: Fsub_Soundness.v Fsub_Lemmas.vo
|
||||||
|
Fsub_Soundness.vio: Fsub_Soundness.v Fsub_Lemmas.vio
|
||||||
|
Fsub_Soundness.vos Fsub_Soundness.vok Fsub_Soundness.required_vos: Fsub_Soundness.v Fsub_Lemmas.vos
|
||||||
109
share/popl08-tutorial-Fsub/AdditionalTactics.v.crashcoqide
Normal file
|
|
@ -0,0 +1,109 @@
|
||||||
|
(** A library of additional tactics. *)
|
||||||
|
|
||||||
|
Require Export String.
|
||||||
|
Open Scope string_scope.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * Extensions of the standard library *)
|
||||||
|
|
||||||
|
(** "[remember c as x in |-]" replaces the term [c] by the identifier
|
||||||
|
[x] in the conclusion of the current goal and introduces the
|
||||||
|
hypothesis [x=c] into the context. This tactic differs from a
|
||||||
|
similar one in the standard library in that the replacmement is
|
||||||
|
made only in the conclusion of the goal; the context is left
|
||||||
|
unchanged. *)
|
||||||
|
|
||||||
|
Tactic Notation "remember" constr(c) "as" ident(x) "in" "|-" :=
|
||||||
|
let x := fresh x in
|
||||||
|
let H := fresh "Heq" x in
|
||||||
|
(set (x := c); assert (H : x = c) by reflexivity; clearbody x).
|
||||||
|
|
||||||
|
(** "[unsimpl E]" replaces all occurence of [X] by [E], where [X] is
|
||||||
|
the result that tactic [simpl] would give when used to evaluate
|
||||||
|
[E]. *)
|
||||||
|
|
||||||
|
Tactic Notation "unsimpl" constr(E) :=
|
||||||
|
let F := (eval simpl in E) in change F with E.
|
||||||
|
|
||||||
|
(** The following tactic calls the [apply] tactic with the first
|
||||||
|
hypothesis that succeeds, "first" meaning the hypothesis that
|
||||||
|
comes earlist in the context (i.e., higher up in the list). *)
|
||||||
|
|
||||||
|
Ltac apply_first_hyp :=
|
||||||
|
match reverse goal with
|
||||||
|
| H : _ |- _ => apply H
|
||||||
|
end.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * Variations on [auto] *)
|
||||||
|
|
||||||
|
(** The [auto*] and [eauto*] tactics are intended to be "stronger"
|
||||||
|
versions of the [auto] and [eauto] tactics. Similar to [auto] and
|
||||||
|
[eauto], they each take an optional "depth" argument. Note that
|
||||||
|
if we declare these tactics using a single string, e.g., "auto*",
|
||||||
|
then the resulting tactics are unusable since they fail to
|
||||||
|
parse. *)
|
||||||
|
|
||||||
|
Tactic Notation "auto" "*" :=
|
||||||
|
try solve [ congruence | auto | intuition auto ].
|
||||||
|
|
||||||
|
Tactic Notation "auto" "*" integer(n) :=
|
||||||
|
try solve [ congruence | auto n | intuition (auto n) ].
|
||||||
|
|
||||||
|
Tactic Notation "eauto" "*" :=
|
||||||
|
try solve [ congruence | eauto | intuition eauto ].
|
||||||
|
|
||||||
|
Tactic Notation "eauto" "*" integer(n) :=
|
||||||
|
try solve [ congruence | eauto n | intuition (eauto n) ].
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * Delineating cases in proofs *)
|
||||||
|
|
||||||
|
(** This section was taken from the POPLmark Wiki
|
||||||
|
( http://alliance.seas.upenn.edu/~plclub/cgi-bin/poplmark/ ). *)
|
||||||
|
|
||||||
|
(** ** Tactic definitions *)
|
||||||
|
|
||||||
|
Ltac move_to_top x :=
|
||||||
|
match reverse goal with
|
||||||
|
| H : _ |- _ => try move x after H
|
||||||
|
end.
|
||||||
|
|
||||||
|
Tactic Notation "assert_eq" ident(x) constr(v) :=
|
||||||
|
let H := fresh in
|
||||||
|
assert (x = v) as H by reflexivity;
|
||||||
|
clear H.
|
||||||
|
|
||||||
|
Tactic Notation "Case_aux" ident(x) constr(name) :=
|
||||||
|
first [
|
||||||
|
set (x := name); move_to_top x
|
||||||
|
| assert_eq x name
|
||||||
|
| fail 1 "because we are working on a different case." ].
|
||||||
|
|
||||||
|
Ltac Case name := Case_aux case name.
|
||||||
|
Ltac SCase name := Case_aux subcase name.
|
||||||
|
Ltac SSCase name := Case_aux subsubcase name.
|
||||||
|
|
||||||
|
(** ** Example
|
||||||
|
|
||||||
|
One mode of use for the above tactics is to wrap Coq's [induction]
|
||||||
|
tactic such that automatically inserts "case" markers into each
|
||||||
|
branch of the proof. For example:
|
||||||
|
|
||||||
|
<<
|
||||||
|
Tactic Notation "induction" "nat" ident(n) :=
|
||||||
|
induction n; [ Case "O" | Case "S" ].
|
||||||
|
Tactic Notation "sub" "induction" "nat" ident(n) :=
|
||||||
|
induction n; [ SCase "O" | SCase "S" ].
|
||||||
|
Tactic Notation "sub" "sub" "induction" "nat" ident(n) :=
|
||||||
|
induction n; [ SSCase "O" | SSCase "S" ].
|
||||||
|
>>
|
||||||
|
|
||||||
|
If you use such customized versions of the induction tactics, then
|
||||||
|
the [Case] tactic will verify that you are working on the case
|
||||||
|
that you think you are. You may also use the [Case] tactic with
|
||||||
|
the standard version of [induction], in which case no verification
|
||||||
|
is done. *)
|
||||||
265
share/popl08-tutorial-Fsub/Atom.v.crashcoqide
Normal file
|
|
@ -0,0 +1,265 @@
|
||||||
|
(** Support for atoms, i.e., objects with decidable equality. We
|
||||||
|
provide here the ability to generate an atom fresh for any finite
|
||||||
|
collection, e.g., the lemma [atom_fresh_for_set], and a tactic to
|
||||||
|
pick an atom fresh for the current proof context.
|
||||||
|
|
||||||
|
Authors: Arthur Charguéraud and Brian Aydemir.
|
||||||
|
|
||||||
|
Implementation note: In older versions of Coq, [OrderedTypeEx]
|
||||||
|
redefines decimal constants to be integers and not natural
|
||||||
|
numbers. The following scope declaration is intended to address
|
||||||
|
this issue. In newer versions of Coq, the declaration should be
|
||||||
|
benign. *)
|
||||||
|
|
||||||
|
Require Import List.
|
||||||
|
(*Require Import Max.*)
|
||||||
|
Require Import OrderedType.
|
||||||
|
Require Import OrderedTypeEx.
|
||||||
|
Open Scope nat_scope.
|
||||||
|
|
||||||
|
Require Import FiniteSets.
|
||||||
|
Require Import FSetDecide.
|
||||||
|
Require Import FSetNotin.
|
||||||
|
Require Import ListFacts.
|
||||||
|
Require Import Psatz.
|
||||||
|
|
||||||
|
Require Import AdditionalTactics.
|
||||||
|
Require AdditionalTactics.
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * Definition *)
|
||||||
|
|
||||||
|
(** Atoms are structureless objects such that we can always generate
|
||||||
|
one fresh from a finite collection. Equality on atoms is [eq] and
|
||||||
|
decidable. We use Coq's module system to make abstract the
|
||||||
|
implementation of atoms. The [Export AtomImpl] line below allows
|
||||||
|
us to refer to the type [atom] and its properties without having
|
||||||
|
to qualify everything with "[AtomImpl.]". *)
|
||||||
|
|
||||||
|
Module Type ATOM.
|
||||||
|
|
||||||
|
Parameter atom : Set.
|
||||||
|
|
||||||
|
Parameter atom_fresh_for_list :
|
||||||
|
forall (xs : list atom), {x : atom | ~ List.In x xs}.
|
||||||
|
|
||||||
|
Declare Module Atom_as_OT : UsualOrderedType with Definition t := atom.
|
||||||
|
|
||||||
|
Parameter eq_atom_dec : forall x y : atom, {x = y} + {x <> y}.
|
||||||
|
|
||||||
|
End ATOM.
|
||||||
|
|
||||||
|
(** The implementation of the above interface is hidden for
|
||||||
|
documentation purposes. *)
|
||||||
|
|
||||||
|
Module AtomImpl : ATOM.
|
||||||
|
|
||||||
|
(* begin hide *)
|
||||||
|
|
||||||
|
Definition atom := nat.
|
||||||
|
|
||||||
|
Lemma max_lt_r : forall x y z,
|
||||||
|
x <= z -> x <= max y z.
|
||||||
|
Proof.
|
||||||
|
induction x. auto with arith.
|
||||||
|
induction y; auto with arith.
|
||||||
|
simpl. induction z. lia. auto with arith.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma nat_list_max : forall (xs : list nat),
|
||||||
|
{ n : nat | forall x, In x xs -> x <= n }.
|
||||||
|
Proof.
|
||||||
|
induction xs as [ | x xs [y H] ].
|
||||||
|
(* case: nil *)
|
||||||
|
exists 0. inversion 1.
|
||||||
|
(* case: cons x xs *)
|
||||||
|
exists (max x y). intros z J. simpl in J. destruct J as [K | K].
|
||||||
|
subst. auto with arith.
|
||||||
|
auto using max_lt_r.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma atom_fresh_for_list :
|
||||||
|
forall (xs : list nat), { n : nat | ~ List.In n xs }.
|
||||||
|
Proof.
|
||||||
|
intros xs. destruct (nat_list_max xs) as [x H].
|
||||||
|
exists (S x). intros J. lapply (H (S x)). lia. trivial.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Module Atom_as_OT := Nat_as_OT.
|
||||||
|
Module Facts := OrderedTypeFacts Atom_as_OT.
|
||||||
|
|
||||||
|
Definition eq_atom_dec : forall x y : atom, {x = y} + {x <> y} :=
|
||||||
|
Facts.eq_dec.
|
||||||
|
|
||||||
|
(* end hide *)
|
||||||
|
|
||||||
|
End AtomImpl.
|
||||||
|
|
||||||
|
Export AtomImpl.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * Finite sets of atoms *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Definitions *)
|
||||||
|
|
||||||
|
Module AtomSet : FiniteSets.S with Module E := Atom_as_OT :=
|
||||||
|
FiniteSets.Make Atom_as_OT.
|
||||||
|
|
||||||
|
(** The type [atoms] is the type of finite sets of [atom]s. *)
|
||||||
|
|
||||||
|
Notation atoms := AtomSet.F.t.
|
||||||
|
|
||||||
|
(** Basic operations on finite sets of atoms are available, in the
|
||||||
|
remainder of this file, without qualification. We use [Import]
|
||||||
|
instead of [Export] in order to avoid unnecessary namespace
|
||||||
|
pollution. *)
|
||||||
|
|
||||||
|
Import AtomSet.F.
|
||||||
|
|
||||||
|
(** We instantiate two modules which provide useful lemmas and tactics
|
||||||
|
work working with finite sets of atoms. *)
|
||||||
|
|
||||||
|
Module AtomSetDecide := FSetDecide.Decide AtomSet.F.
|
||||||
|
Module AtomSetNotin := FSetNotin.Notin AtomSet.F.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** ** Tactics for working with finite sets of atoms *)
|
||||||
|
|
||||||
|
(** The tactic [fsetdec] is a general purpose decision procedure
|
||||||
|
for solving facts about finite sets of atoms. *)
|
||||||
|
|
||||||
|
Ltac fsetdec := try apply AtomSet.eq_if_Equal; AtomSetDecide.fsetdec.
|
||||||
|
|
||||||
|
(** The tactic [notin_simpl] simplifies all hypotheses of the form [(~
|
||||||
|
In x F)], where [F] is constructed from the empty set, singleton
|
||||||
|
sets, and unions. *)
|
||||||
|
|
||||||
|
Ltac notin_simpl := AtomSetNotin.notin_simpl_hyps.
|
||||||
|
|
||||||
|
(** The tactic [notin_solve], solves goals of the form [(~ In x F)],
|
||||||
|
where [F] is constructed from the empty set, singleton sets, and
|
||||||
|
unions. The goal must be provable from hypothesis of the form
|
||||||
|
simplified by [notin_simpl]. *)
|
||||||
|
|
||||||
|
Ltac notin_solve := AtomSetNotin.notin_solve.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** ** Lemmas for working with finite sets of atoms *)
|
||||||
|
|
||||||
|
(** We make some lemmas about finite sets of atoms available without
|
||||||
|
qualification by using abbreviations. *)
|
||||||
|
|
||||||
|
Notation eq_if_Equal := AtomSet.eq_if_Equal.
|
||||||
|
Notation notin_empty := AtomSetNotin.notin_empty.
|
||||||
|
Notation notin_singleton := AtomSetNotin.notin_singleton.
|
||||||
|
Notation notin_singleton_rw := AtomSetNotin.notin_singleton_rw.
|
||||||
|
Notation notin_union := AtomSetNotin.notin_union.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * Additional properties *)
|
||||||
|
|
||||||
|
(** One can generate an atom fresh for a given finite set of atoms. *)
|
||||||
|
|
||||||
|
Lemma atom_fresh_for_set : forall L : atoms, { x : atom | ~ In x L }.
|
||||||
|
Proof.
|
||||||
|
intros L. destruct (atom_fresh_for_list (elements L)) as [a H].
|
||||||
|
exists a. intros J. contradiction H.
|
||||||
|
rewrite <- InA_iff_In. auto using elements_1.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * Additional tactics *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** #<a name="pick_fresh"></a># Picking a fresh atom *)
|
||||||
|
|
||||||
|
(** We define three tactics which, when combined, provide a simple
|
||||||
|
mechanism for picking a fresh atom. We demonstrate their use
|
||||||
|
below with an example, the [example_pick_fresh] tactic.
|
||||||
|
|
||||||
|
[(gather_atoms_with F)] returns the union of [(F x)], where [x]
|
||||||
|
ranges over all objects in the context such that [(F x)] is
|
||||||
|
well typed. The return type of [F] should be [atoms]. The
|
||||||
|
complexity of this tactic is due to the fact that there is no
|
||||||
|
support in [Ltac] for folding a function over the context. *)
|
||||||
|
|
||||||
|
Ltac gather_atoms_with F :=
|
||||||
|
let rec gather V :=
|
||||||
|
match goal with
|
||||||
|
| H: ?S |- _ =>
|
||||||
|
let FH := constr:(F H) in
|
||||||
|
match V with
|
||||||
|
| empty => gather FH
|
||||||
|
| context [FH] => fail 1
|
||||||
|
| _ => gather (union FH V)
|
||||||
|
end
|
||||||
|
| _ => V
|
||||||
|
end in
|
||||||
|
let L := gather empty in eval simpl in L.
|
||||||
|
|
||||||
|
(** [(beautify_fset V)] takes a set [V] built as a union of finite
|
||||||
|
sets and returns the same set with empty sets removed and union
|
||||||
|
operations associated to the right. Duplicate sets are also
|
||||||
|
removed from the union. *)
|
||||||
|
|
||||||
|
Ltac beautify_fset V :=
|
||||||
|
let rec go Acc E :=
|
||||||
|
match E with
|
||||||
|
| union ?E1 ?E2 => let Acc1 := go Acc E2 in go Acc1 E1
|
||||||
|
| empty => Acc
|
||||||
|
| ?E1 => match Acc with
|
||||||
|
| empty => E1
|
||||||
|
| context [E1] => Acc
|
||||||
|
| _ => constr:(union E1 Acc)
|
||||||
|
end
|
||||||
|
end
|
||||||
|
in go empty V.
|
||||||
|
|
||||||
|
(** The tactic [(pick fresh Y for L)] takes a finite set of atoms [L]
|
||||||
|
and a fresh name [Y], and adds to the context an atom with name
|
||||||
|
[Y] and a proof that [(~ In Y L)], i.e., that [Y] is fresh for
|
||||||
|
[L]. The tactic will fail if [Y] is already declared in the
|
||||||
|
context. *)
|
||||||
|
|
||||||
|
Tactic Notation "pick" "fresh" ident(Y) "for" constr(L) :=
|
||||||
|
let Fr := fresh "Fr" in
|
||||||
|
let L := beautify_fset L in
|
||||||
|
(destruct (atom_fresh_for_set L) as [Y Fr]).
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Demonstration *)
|
||||||
|
|
||||||
|
(** The [example_pick_fresh] tactic below illustrates the general
|
||||||
|
pattern for using the above three tactics to define a tactic which
|
||||||
|
picks a fresh atom. The pattern is as follows:
|
||||||
|
- Repeatedly invoke [gather_atoms_with], using functions with
|
||||||
|
different argument types each time.
|
||||||
|
- Union together the result of the calls, and invoke
|
||||||
|
[(pick fresh ... for ...)] with that union of sets. *)
|
||||||
|
|
||||||
|
Ltac example_pick_fresh Y :=
|
||||||
|
let A := gather_atoms_with (fun x : atoms => x) in
|
||||||
|
let B := gather_atoms_with (fun x : atom => singleton x) in
|
||||||
|
pick fresh Y for (union A B).
|
||||||
|
|
||||||
|
Lemma example_pick_fresh_use : forall (x y z : atom) (L1 L2 L3: atoms), True.
|
||||||
|
(* begin show *)
|
||||||
|
Proof.
|
||||||
|
intros x y z L1 L2 L3. example_pick_fresh k.
|
||||||
|
|
||||||
|
(** At this point in the proof, we have a new atom [k] and a
|
||||||
|
hypothesis [Fr : ~ In k (union L1 (union L2 (union L3 (union
|
||||||
|
(singleton x) (union (singleton y) (singleton z))))))]. *)
|
||||||
|
|
||||||
|
trivial.
|
||||||
|
Qed.
|
||||||
|
(* end show *)
|
||||||
697
share/popl08-tutorial-Fsub/Environment.v.crashcoqide
Normal file
|
|
@ -0,0 +1,697 @@
|
||||||
|
(** Operations, lemmas, and tactics for working with environments,
|
||||||
|
association lists whose keys are atoms. Unless stated otherwise,
|
||||||
|
implicit arguments will not be declared by default.
|
||||||
|
|
||||||
|
Authors: Brian Aydemir and Arthur Charguéraud, with help from
|
||||||
|
Aaron Bohannon, Benjamin Pierce, Jeffrey Vaughan, Dimitrios
|
||||||
|
Vytiniotis, Stephanie Weirich, and Steve Zdancewic.
|
||||||
|
|
||||||
|
Table of contents:
|
||||||
|
- #<a href="##overview">Overview</a>#
|
||||||
|
- #<a href="##functions">Functions on environments</a>#
|
||||||
|
- #<a href="##env_rel">Relations on environments</a>#
|
||||||
|
- #<a href="##op_prop">Properties of operations</a>#
|
||||||
|
- #<a href="##auto1">Automation and tactics (I)</a>#
|
||||||
|
- #<a href="##props">Properties of well-formedness and freshness</a>#
|
||||||
|
- #<a href="##binds_prop">Properties of binds</a>#
|
||||||
|
- #<a href="##auto2">Automation and tactics (II)</a>#
|
||||||
|
- #<a href="##binds_prop2">Additional properties of binds</a>#
|
||||||
|
- #<a href="##auto3">Automation and tactics (III)</a># *)
|
||||||
|
|
||||||
|
Require Export List.
|
||||||
|
Require Export ListFacts.
|
||||||
|
Require Import Atom.
|
||||||
|
|
||||||
|
Require Import Coq.Lists.List.
|
||||||
|
Include ListNotations.
|
||||||
|
|
||||||
|
Import AtomSet.F.
|
||||||
|
|
||||||
|
Create HintDb EnvHints.
|
||||||
|
Local Hint Unfold E.eq : EnvHints.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="overview"></a># Overview *)
|
||||||
|
|
||||||
|
(** An environment is a list of pairs, where the first component of
|
||||||
|
each pair is an [atom]. We view the second component of each pair
|
||||||
|
as being bound to the first component. In a well-formed
|
||||||
|
environment, there is at most one binding for any given atom.
|
||||||
|
Bindings at the head of the list are "more recent" than bindings
|
||||||
|
toward the tail of the list, and we view an environment as growing
|
||||||
|
on the left, i.e., at its head.
|
||||||
|
|
||||||
|
We normally work only with environments built up from the
|
||||||
|
following: the empty list, one element lists, and concatenations
|
||||||
|
of two lists. This seems to be more convenient in practice. For
|
||||||
|
example, we don't need to distinguish between consing on a binding
|
||||||
|
and concatenating a binding, a difference that Coq's tactics can
|
||||||
|
be sensitive to.
|
||||||
|
|
||||||
|
However, basic definitions are by induction on the usual structure
|
||||||
|
of lists ([nil] and [cons]).
|
||||||
|
|
||||||
|
To make it convenient to write one element lists, we define a
|
||||||
|
special notation. Note that this notation is local to this
|
||||||
|
particular library, to allow users to use alternate notations if
|
||||||
|
they desire. *)
|
||||||
|
|
||||||
|
Local Notation "[ x ]" := (cons x nil).
|
||||||
|
|
||||||
|
(** In the remainder of this library, we define a number of
|
||||||
|
operations, lemmas, and tactics that simplify working with
|
||||||
|
environments. *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="functions"></a># Functions on environments *)
|
||||||
|
|
||||||
|
(** Implicit arguments will be declared by default for the definitions
|
||||||
|
in this section. *)
|
||||||
|
|
||||||
|
Set Implicit Arguments.
|
||||||
|
|
||||||
|
Section Definitions.
|
||||||
|
|
||||||
|
Variables A B : Type.
|
||||||
|
|
||||||
|
(** The domain of an environment is the set of atoms that it maps. *)
|
||||||
|
|
||||||
|
Fixpoint dom (E : list (atom * A)) : atoms :=
|
||||||
|
match E with
|
||||||
|
| nil => empty
|
||||||
|
| (x, _) :: E' => union (singleton x) (dom E')
|
||||||
|
end.
|
||||||
|
|
||||||
|
(** [map] applies a function to all bindings in the environment. *)
|
||||||
|
|
||||||
|
Fixpoint map (f : A -> B) (E : list (atom * A)) : list (atom * B) :=
|
||||||
|
match E with
|
||||||
|
| nil => nil
|
||||||
|
| (x, V) :: E' => (x, f V) :: map f E'
|
||||||
|
end.
|
||||||
|
|
||||||
|
(** [get] returns the value bound to the given atom in an environment
|
||||||
|
or [None] if the given atom is not bound. If the atom has
|
||||||
|
multiple bindings, the one nearest to the head of the environment
|
||||||
|
is returned. *)
|
||||||
|
|
||||||
|
Fixpoint get (x : atom) (E : list (atom * A)) : option A :=
|
||||||
|
match E with
|
||||||
|
| nil => None
|
||||||
|
| (y,a) :: E' => if eq_atom_dec x y then Some a else get x E'
|
||||||
|
end.
|
||||||
|
|
||||||
|
End Definitions.
|
||||||
|
|
||||||
|
Unset Implicit Arguments.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="env_rel"></a># Relations on environments *)
|
||||||
|
|
||||||
|
(** Implicit arguments will be declared by default for the definitions
|
||||||
|
in this section. *)
|
||||||
|
|
||||||
|
Set Implicit Arguments.
|
||||||
|
|
||||||
|
Section Relations.
|
||||||
|
|
||||||
|
Variable A : Type.
|
||||||
|
|
||||||
|
(** An environment is well-formed if and only if each atom is bound at
|
||||||
|
most once. *)
|
||||||
|
|
||||||
|
Inductive ok : list (atom * A) -> Prop :=
|
||||||
|
| ok_nil :
|
||||||
|
ok nil
|
||||||
|
| ok_cons : forall (E : list (atom * A)) (x : atom) (a : A),
|
||||||
|
ok E -> ~ In x (dom E) -> ok ((x, a) :: E).
|
||||||
|
|
||||||
|
(** #<a name="binds_doc"></a># An environment [E] contains a binding
|
||||||
|
from [x] to [b], denoted [(binds x b E)], if and only if the most
|
||||||
|
recent binding for [x] is mapped to [b]. *)
|
||||||
|
|
||||||
|
Definition binds x b (E : list (atom * A)) :=
|
||||||
|
get x E = Some b.
|
||||||
|
|
||||||
|
End Relations.
|
||||||
|
|
||||||
|
Unset Implicit Arguments.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="op_prop"></a># Properties of operations *)
|
||||||
|
|
||||||
|
Section OpProperties.
|
||||||
|
Variable A B : Type.
|
||||||
|
Implicit Types E F : list (atom * A).
|
||||||
|
Implicit Types a b : A.
|
||||||
|
|
||||||
|
(** ** Facts about concatenation *)
|
||||||
|
|
||||||
|
Lemma concat_nil : forall E,
|
||||||
|
(E ++ nil) = E.
|
||||||
|
Proof.
|
||||||
|
auto using List.app_nil_r.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma nil_concat : forall E,
|
||||||
|
nil ++ E = E.
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma concat_assoc : forall E F G,
|
||||||
|
(G ++ F) ++ E = G ++ (F ++ E).
|
||||||
|
Proof.
|
||||||
|
auto using List.app_assoc.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** ** [map] commutes with environment-building operations *)
|
||||||
|
|
||||||
|
Lemma map_nil : forall (f : A -> B),
|
||||||
|
map f nil = nil.
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma map_single : forall (f : A -> B) y b,
|
||||||
|
map f [(y,b)] = [(y, f b)].
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma map_push : forall (f : A -> B) y b E,
|
||||||
|
map f ([(y,b)] ++ E) = [(y, f b)] ++ map f E.
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma map_concat : forall (f : A -> B) E F,
|
||||||
|
map f (F ++ E) = (map f F) ++ (map f E).
|
||||||
|
Proof.
|
||||||
|
induction F as [|(x,a)]; simpl; congruence.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** ** Facts about the domain of an environment *)
|
||||||
|
|
||||||
|
Lemma dom_nil :
|
||||||
|
@dom A nil = empty.
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma dom_single : forall x a,
|
||||||
|
dom [(x,a)] = singleton x.
|
||||||
|
Proof.
|
||||||
|
simpl. intros.
|
||||||
|
Admitted.
|
||||||
|
(* fsetdec.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma dom_push : forall x a E,
|
||||||
|
dom ([(x,a)] ++ E) = union (singleton x) (dom E).
|
||||||
|
Proof.
|
||||||
|
simpl. intros. reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma dom_concat : forall E F,
|
||||||
|
dom (F ++ E) = union (dom F) (dom E).
|
||||||
|
Proof.
|
||||||
|
induction F as [|(x,a) F IH]; simpl.
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
fsetdec.
|
||||||
|
rewrite IH.
|
||||||
|
fsetdec.
|
||||||
|
Qed.*)
|
||||||
|
|
||||||
|
Lemma dom_map : forall (f : A -> B) E,
|
||||||
|
dom (map f E) = dom E.
|
||||||
|
Proof.
|
||||||
|
induction E as [|(x,a)]; simpl; congruence.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** ** Other trivial rewrites *)
|
||||||
|
|
||||||
|
Lemma cons_concat_assoc : forall x a E F,
|
||||||
|
((x, a) :: E) ++ F = (x, a) :: (E ++ F).
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
End OpProperties.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="auto1"></a># Automation and tactics (I) *)
|
||||||
|
|
||||||
|
(** ** [simpl_env] *)
|
||||||
|
|
||||||
|
(** The [simpl_env] tactic can be used to put environments in the
|
||||||
|
standardized form described above, with the additional properties
|
||||||
|
that concatenation is associated to the right and empty
|
||||||
|
environments are removed. Similar to the [simpl] tactic, we
|
||||||
|
define "[in *]" and "[in H]" variants of [simpl_env]. *)
|
||||||
|
|
||||||
|
Definition singleton_list (A : Type) (x : atom * A) := x :: nil.
|
||||||
|
|
||||||
|
Arguments singleton_list [A].
|
||||||
|
|
||||||
|
Lemma cons_concat : forall (A : Type) (E : list (atom * A)) x a,
|
||||||
|
(x, a) :: E = singleton_list (x, a) ++ E.
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma map_singleton_list : forall (A B : Type) (f : A -> B) y b,
|
||||||
|
map f (singleton_list (y,b)) = [(y, f b)].
|
||||||
|
Proof.
|
||||||
|
reflexivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma dom_singleton_list : forall (A : Type) (x : atom) (a : A),
|
||||||
|
dom (singleton_list (x,a)) = singleton x.
|
||||||
|
Proof.
|
||||||
|
simpl. intros.
|
||||||
|
Admitted.
|
||||||
|
(* fsetdec.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Hint Rewrite
|
||||||
|
cons_concat map_singleton_list dom_singleton_list
|
||||||
|
concat_nil nil_concat concat_assoc
|
||||||
|
map_nil map_single map_push map_concat
|
||||||
|
dom_nil dom_single dom_push dom_concat dom_map : rew_env.
|
||||||
|
|
||||||
|
Ltac simpl_env_change_aux :=
|
||||||
|
match goal with
|
||||||
|
| H : context[?x :: nil] |- _ =>
|
||||||
|
progress (change (x :: nil) with (singleton_list x) in H);
|
||||||
|
simpl_env_change_aux
|
||||||
|
| |- context[?x :: nil] =>
|
||||||
|
progress (change (x :: nil) with (singleton_list x));
|
||||||
|
simpl_env_change_aux
|
||||||
|
| _ =>
|
||||||
|
idtac
|
||||||
|
end.
|
||||||
|
|
||||||
|
Ltac simpl_env :=
|
||||||
|
simpl_env_change_aux;
|
||||||
|
autorewrite with rew_env;
|
||||||
|
unfold singleton_list in *.
|
||||||
|
|
||||||
|
Tactic Notation "simpl_env" "in" hyp(H) :=
|
||||||
|
simpl_env_change_aux;
|
||||||
|
autorewrite with rew_env in H;
|
||||||
|
unfold singleton_list in *.
|
||||||
|
|
||||||
|
Tactic Notation "simpl_env" "in" "*" :=
|
||||||
|
simpl_env_change_aux;
|
||||||
|
autorewrite with rew_env in *;
|
||||||
|
unfold singleton_list in *.
|
||||||
|
|
||||||
|
(** ** [rewrite_env] *)
|
||||||
|
|
||||||
|
(** The tactic [(rewrite_env E)] replaces an environment in the
|
||||||
|
conclusion of the goal with [E]. Suitability for replacement is
|
||||||
|
determined by whether [simpl_env] can put [E] and the chosen
|
||||||
|
environment in the same normal form, up to convertability in Coq.
|
||||||
|
We also define a "[in H]" variant that performs the replacement in
|
||||||
|
a hypothesis [H]. *)
|
||||||
|
|
||||||
|
Tactic Notation "rewrite_env" constr(E) :=
|
||||||
|
match goal with
|
||||||
|
| |- context[?x] =>
|
||||||
|
change x with E
|
||||||
|
| |- context[?x] =>
|
||||||
|
replace x with E; [ | try reflexivity; simpl_env; reflexivity ]
|
||||||
|
end.
|
||||||
|
|
||||||
|
Tactic Notation "rewrite_env" constr(E) "in" hyp(H) :=
|
||||||
|
match type of H with
|
||||||
|
| context[?x] =>
|
||||||
|
change x with E in H
|
||||||
|
| context[?x] =>
|
||||||
|
replace x with E in H; [ | try reflexivity; simpl_env; reflexivity ]
|
||||||
|
end.
|
||||||
|
|
||||||
|
(** ** Hints *)
|
||||||
|
|
||||||
|
Hint Constructors ok :EnvHints.
|
||||||
|
|
||||||
|
Local Hint Extern 1 (~ In _ _) => simpl_env in * : fsetdec.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="props"></a># Properties of well-formedness and freshness *)
|
||||||
|
|
||||||
|
Section OkProperties.
|
||||||
|
Variable A B : Type.
|
||||||
|
Implicit Types E F : list (atom * A).
|
||||||
|
Implicit Types a b : A.
|
||||||
|
|
||||||
|
(** Facts about when an environment is well-formed. *)
|
||||||
|
|
||||||
|
Lemma ok_push : forall (E : list (atom * A)) (x : atom) (a : A),
|
||||||
|
ok E -> ~ In x (dom E) -> ok ([(x, a)] ++ E).
|
||||||
|
Proof.
|
||||||
|
exact (@ok_cons A).
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma ok_singleton : forall x a,
|
||||||
|
ok [(x,a)].
|
||||||
|
Proof.
|
||||||
|
auto.
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
Lemma ok_remove_mid : forall F E G,
|
||||||
|
ok (G ++ F ++ E) -> ok (G ++ E).
|
||||||
|
Proof with auto.
|
||||||
|
induction G as [|(y,a)]; intros Ok.
|
||||||
|
induction F as [|(y,a)]; simpl... inversion Ok...
|
||||||
|
inversion Ok. simpl...
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma ok_remove_mid_cons : forall x a E G,
|
||||||
|
ok (G ++ (x, a) :: E) ->
|
||||||
|
ok (G ++ E).
|
||||||
|
Proof.
|
||||||
|
intros. simpl_env in *. eauto using ok_remove_mid.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma ok_map : forall E (f : A -> B),
|
||||||
|
ok E -> ok (map f E).
|
||||||
|
Proof with auto.
|
||||||
|
intros.
|
||||||
|
induction E as [ | (y,b) E ] ; simpl...
|
||||||
|
inversion H...
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma ok_map_app_l : forall E F (f : A -> A),
|
||||||
|
ok (F ++ E) -> ok (map f F ++ E).
|
||||||
|
Proof with auto.
|
||||||
|
intros. induction F as [|(y,a)]; simpl...
|
||||||
|
inversion H...
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
(** A binding in the middle of an environment has an atom fresh from
|
||||||
|
all bindings before and after it. *)
|
||||||
|
|
||||||
|
Lemma fresh_mid_tail : forall E F x a,
|
||||||
|
ok (F ++ [(x,a)] ++ E) -> ~ In x (dom E).
|
||||||
|
Proof with auto.
|
||||||
|
induction F as [|(y,b)]; intros x c Ok; simpl_env in *.
|
||||||
|
inversion Ok...
|
||||||
|
inversion Ok; subst. simpl_env in *. apply (IHF _ _ H1).
|
||||||
|
assumption.
|
||||||
|
assumption.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma fresh_mid_head : forall E F x a,
|
||||||
|
ok (F ++ [(x,a)] ++ E) -> ~ In x (dom F).
|
||||||
|
Proof with auto.
|
||||||
|
induction F as [|(y,b)]; intros x c Ok; simpl_env in *.
|
||||||
|
inversion Ok...
|
||||||
|
inversion Ok; subst. simpl_env in *.
|
||||||
|
Admitted.
|
||||||
|
(* pose proof (IHF _ _ H1)...
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
End OkProperties.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="binds_prop"></a># Properties of [binds] *)
|
||||||
|
|
||||||
|
Section BindsProperties.
|
||||||
|
Variable A B : Type.
|
||||||
|
Implicit Types E F : list (atom * A).
|
||||||
|
Implicit Types a b : A.
|
||||||
|
|
||||||
|
(** ** Introduction forms for [binds] *)
|
||||||
|
|
||||||
|
(** The following properties allow one to view [binds] as an
|
||||||
|
inductively defined predicate. This is the preferred way of
|
||||||
|
working with the relation. *)
|
||||||
|
|
||||||
|
Lemma binds_singleton : forall x a,
|
||||||
|
binds x a [(x,a)].
|
||||||
|
Proof.
|
||||||
|
intros x a. unfold binds. simpl. destruct (eq_atom_dec x x); intuition.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma binds_tail : forall x a E F,
|
||||||
|
binds x a E -> ~ In x (dom F) -> binds x a (F ++ E).
|
||||||
|
Proof with auto.
|
||||||
|
unfold binds. induction F as [|(y,b)]; simpl...
|
||||||
|
destruct (eq_atom_dec x y)... intros _ J. destruct J.
|
||||||
|
Admitted.
|
||||||
|
(* fsetdec.
|
||||||
|
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma binds_head : forall x a E F,
|
||||||
|
binds x a F -> binds x a (F ++ E).
|
||||||
|
Proof.
|
||||||
|
unfold binds. induction F as [|(y,b)]; simpl; intros H.
|
||||||
|
discriminate.
|
||||||
|
destruct (eq_atom_dec x y); intuition.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** ** Case analysis on [binds] *)
|
||||||
|
|
||||||
|
Lemma binds_concat_inv : forall x a E F,
|
||||||
|
binds x a (F ++ E) -> (~ In x (dom F) /\ binds x a E) \/ (binds x a F).
|
||||||
|
Proof with auto.
|
||||||
|
unfold binds. induction F as [|(y,b)]; simpl; intros H...
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
destruct (eq_atom_dec x y).
|
||||||
|
right...
|
||||||
|
destruct (IHF H) as [[? ?] | ?]. left... right...
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma binds_singleton_inv : forall x y a b,
|
||||||
|
binds x a [(y,b)] -> x = y /\ a = b.
|
||||||
|
Proof.
|
||||||
|
unfold binds. simpl. intros. destruct (eq_atom_dec x y).
|
||||||
|
split; congruence.
|
||||||
|
discriminate.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** ** Retrieving bindings from an environment *)
|
||||||
|
|
||||||
|
Lemma binds_mid : forall x a E F,
|
||||||
|
ok (F ++ [(x,a)] ++ E) -> binds x a (F ++ [(x,a)] ++ E).
|
||||||
|
Proof with auto.
|
||||||
|
unfold binds. induction F as [|(z,b)]; simpl; intros Ok.
|
||||||
|
destruct (eq_atom_dec x x); intuition.
|
||||||
|
inversion Ok; subst. destruct (eq_atom_dec x z)...
|
||||||
|
destruct H3. simpl_env.
|
||||||
|
Admitted.
|
||||||
|
(* fsetdec.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma binds_mid_eq : forall z a b E F,
|
||||||
|
binds z a (F ++ [(z,b)] ++ E) -> ok (F ++ [(z,b)] ++ E) -> a = b.
|
||||||
|
Proof with auto.
|
||||||
|
unfold binds. induction F as [|(x,c)]; simpl; intros H Ok.
|
||||||
|
destruct (eq_atom_dec z z). congruence. intuition.
|
||||||
|
inversion Ok; subst. destruct (eq_atom_dec z x)...
|
||||||
|
destruct H4. simpl_env.
|
||||||
|
Admitted.
|
||||||
|
(* fsetdec.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma binds_mid_eq_cons : forall x a b E F,
|
||||||
|
binds x a (F ++ (x,b) :: E) ->
|
||||||
|
ok (F ++ (x,b) :: E) ->
|
||||||
|
a = b.
|
||||||
|
Proof.
|
||||||
|
intros. simpl_env in *. eauto using binds_mid_eq.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
End BindsProperties.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="auto2"></a># Automation and tactics (II) *)
|
||||||
|
|
||||||
|
(** ** Hints *)
|
||||||
|
|
||||||
|
Hint Immediate ok_remove_mid ok_remove_mid_cons :EnvHints.
|
||||||
|
|
||||||
|
Hint Resolve
|
||||||
|
ok_push ok_singleton ok_map ok_map_app_l
|
||||||
|
binds_singleton binds_head binds_tail :EnvHints.
|
||||||
|
|
||||||
|
(** ** [binds_get] *)
|
||||||
|
|
||||||
|
(** The tactic [(binds_get H)] takes a hypothesis [H] of the form
|
||||||
|
[(binds x a (F ++ [(x,b)] ++ E))] and introduces the equality
|
||||||
|
[a=b] into the context. Then, the tactic checks if the equality
|
||||||
|
is discriminable and otherwise tries substituting [b] for [a].
|
||||||
|
The [auto] tactic is used to show that [(ok (F ++ [(x,b)] ++ E))],
|
||||||
|
which is needed to prove the equality [a=b] from [H]. *)
|
||||||
|
|
||||||
|
Ltac binds_get H :=
|
||||||
|
match type of H with
|
||||||
|
| binds ?z ?a (?F ++ [(?z,?b)] ++ ?E) =>
|
||||||
|
let K := fresh in
|
||||||
|
assert (K : ok (F ++ [(z,b)] ++ E));
|
||||||
|
[ auto
|
||||||
|
| let J := fresh in
|
||||||
|
assert (J := @binds_mid_eq _ _ _ _ _ _ H K);
|
||||||
|
clear K;
|
||||||
|
try discriminate;
|
||||||
|
try match type of J with
|
||||||
|
| ?a = ?b => subst a
|
||||||
|
end
|
||||||
|
]
|
||||||
|
end.
|
||||||
|
|
||||||
|
(** ** [binds_cases] *)
|
||||||
|
|
||||||
|
(** The tactic [(binds_case H)] performs a case analysis on an
|
||||||
|
hypothesis [H] of the form [(binds x a E)]. There will be one
|
||||||
|
subgoal for each component of [E] that [x] could be bound in, and
|
||||||
|
each subgoal will have appropriate freshness conditions on [x].
|
||||||
|
Some attempts are made to automatically discharge contradictory
|
||||||
|
cases. *)
|
||||||
|
|
||||||
|
Ltac binds_cases H :=
|
||||||
|
let Fr := fresh "Fr" in
|
||||||
|
let J1 := fresh in
|
||||||
|
let J2 := fresh in
|
||||||
|
match type of H with
|
||||||
|
| binds _ _ nil =>
|
||||||
|
inversion H
|
||||||
|
| binds ?x ?a [(?y,?b)] =>
|
||||||
|
destruct (@binds_singleton_inv _ _ _ _ _ H);
|
||||||
|
clear H;
|
||||||
|
try discriminate;
|
||||||
|
try subst y;
|
||||||
|
try match goal with
|
||||||
|
| _ : ?z <> ?z |- _ => intuition
|
||||||
|
end
|
||||||
|
| binds ?x ?a (?F ++ ?E) =>
|
||||||
|
destruct (@binds_concat_inv _ _ _ _ _ H) as [[Fr J1] | J2];
|
||||||
|
clear H;
|
||||||
|
[ binds_cases J1 | binds_cases J2 ]
|
||||||
|
| _ => idtac
|
||||||
|
end.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * #<a name="binds_prop2"></a># Additional properties of [binds] *)
|
||||||
|
|
||||||
|
(** The following lemmas are proven in manner that should be
|
||||||
|
independent of the concrete definition of [binds]. *)
|
||||||
|
|
||||||
|
Section AdditionalBindsProperties.
|
||||||
|
Variable A B : Type.
|
||||||
|
Implicit Types E F : list (atom * A).
|
||||||
|
Implicit Types a b : A.
|
||||||
|
|
||||||
|
(** Lemmas about the relationship between [binds] and the domain of an
|
||||||
|
environment. *)
|
||||||
|
|
||||||
|
Lemma binds_In : forall a x E,
|
||||||
|
binds x a E -> In x (dom E).
|
||||||
|
Proof.
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
induction E as [|(y,b)]; simpl_env; intros H.
|
||||||
|
binds_cases H.
|
||||||
|
binds_cases H; subst. auto using union_3. fsetdec.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma binds_fresh : forall x a E,
|
||||||
|
~ In x (dom E) -> ~ binds x a E.
|
||||||
|
Proof.
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
induction E as [|(y,b)]; simpl_env; intros Fresh H.
|
||||||
|
binds_cases H.
|
||||||
|
binds_cases H. intuition. fsetdec.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
(** Additional lemmas for showing that a binding is in an
|
||||||
|
environment. *)
|
||||||
|
|
||||||
|
Lemma binds_map : forall x a (f : A -> B) E,
|
||||||
|
binds x a E -> binds x (f a) (map f E).
|
||||||
|
Proof.
|
||||||
|
induction E as [|(y,b)]; simpl_env; intros H.
|
||||||
|
binds_cases H.
|
||||||
|
binds_cases H; auto. subst; auto.
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma binds_concat_ok : forall x a E F,
|
||||||
|
binds x a E -> ok (F ++ E) -> binds x a (F ++ E).
|
||||||
|
Proof.
|
||||||
|
induction F as [|(y,b)]; simpl_env; intros H Ok.
|
||||||
|
auto.
|
||||||
|
inversion Ok; subst. destruct (eq_atom_dec x y); subst; auto.
|
||||||
|
assert (In y (dom (F ++ E))) by eauto using binds_In.
|
||||||
|
intuition.
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma binds_weaken : forall x a E F G,
|
||||||
|
binds x a (G ++ E) ->
|
||||||
|
ok (G ++ F ++ E) ->
|
||||||
|
binds x a (G ++ F ++ E).
|
||||||
|
Proof.
|
||||||
|
induction G as [|(y,b)]; simpl_env; intros H Ok.
|
||||||
|
auto using binds_concat_ok.
|
||||||
|
inversion Ok; subst. binds_cases H; subst; auto.
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma binds_weaken_at_head : forall x a F G,
|
||||||
|
binds x a G ->
|
||||||
|
ok (F ++ G) ->
|
||||||
|
binds x a (F ++ G).
|
||||||
|
Proof.
|
||||||
|
intros x a F G H J.
|
||||||
|
rewrite_env (nil ++ F ++ G).
|
||||||
|
apply binds_weaken; simpl_env; trivial.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma binds_remove_mid : forall x y a b F G,
|
||||||
|
binds x a (F ++ [(y,b)] ++ G) ->
|
||||||
|
x <> y ->
|
||||||
|
binds x a (F ++ G).
|
||||||
|
Proof.
|
||||||
|
intros x y a b F G H J.
|
||||||
|
binds_cases H; auto.
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma binds_remove_mid_cons : forall x y a b E G,
|
||||||
|
binds x a (G ++ (y, b) :: E) ->
|
||||||
|
x <> y ->
|
||||||
|
binds x a (G ++ E).
|
||||||
|
Proof.
|
||||||
|
intros. simpl_env in *. eauto using binds_remove_mid.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
End AdditionalBindsProperties.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * #<a name="auto3"></a># Automation and tactics (III) *)
|
||||||
|
|
||||||
|
Hint Resolve binds_map binds_concat_ok binds_weaken binds_weaken_at_head :EnvHints.
|
||||||
|
Hint Immediate binds_remove_mid binds_remove_mid_cons :EnvHints.
|
||||||
1057
share/popl08-tutorial-Fsub/FSetDecide.v.crashcoqide
Normal file
183
share/popl08-tutorial-Fsub/FSetNotin.v.crashcoqide
Normal file
|
|
@ -0,0 +1,183 @@
|
||||||
|
(** Lemmas and tactics for working with and solving goals related to
|
||||||
|
non-membership in finite sets. The main tactic of interest here
|
||||||
|
is [notin_solve].
|
||||||
|
|
||||||
|
Authors: Arthur Charguéraud and Brian Aydemir. *)
|
||||||
|
|
||||||
|
Set Implicit Arguments.
|
||||||
|
Require Import FSetInterface.
|
||||||
|
Require Import AdditionalTactics.
|
||||||
|
Require AdditionalTactics.
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * Implementation *)
|
||||||
|
|
||||||
|
Module Notin (X : FSetInterface.S).
|
||||||
|
|
||||||
|
Import X.
|
||||||
|
Import AdditionalTactics.
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** ** Facts about set (non-)membership *)
|
||||||
|
|
||||||
|
Lemma in_singleton : forall x,
|
||||||
|
In x (singleton x).
|
||||||
|
Proof.
|
||||||
|
intros.
|
||||||
|
apply singleton_2.
|
||||||
|
generalize dependent x.
|
||||||
|
apply E.eq_refl.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma notin_empty : forall x,
|
||||||
|
~ In x empty.
|
||||||
|
Proof.
|
||||||
|
auto using empty_1.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma notin_union : forall x E F,
|
||||||
|
~ In x E -> ~ In x F -> ~ In x (union E F).
|
||||||
|
Proof.
|
||||||
|
intros x E F H J K.
|
||||||
|
destruct (union_1 K); intuition.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma elim_notin_union : forall x E F,
|
||||||
|
~ In x (union E F) -> (~ In x E) /\ (~ In x F).
|
||||||
|
Proof.
|
||||||
|
intros x E F H. split; intros J; contradiction H.
|
||||||
|
auto using union_2.
|
||||||
|
auto using union_3.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma notin_singleton : forall x y,
|
||||||
|
~ E.eq x y -> ~ In x (singleton y).
|
||||||
|
Proof.
|
||||||
|
intros x y H J. assert (K := singleton_1 J). auto with *.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma elim_notin_singleton : forall x y,
|
||||||
|
~ In x (singleton y) -> ~ E.eq x y.
|
||||||
|
Proof.
|
||||||
|
intros x y H J.
|
||||||
|
contradiction H.
|
||||||
|
apply singleton_2.
|
||||||
|
generalize x y J.
|
||||||
|
apply E.eq_sym.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma elim_notin_singleton' : forall x y,
|
||||||
|
~ In x (singleton y) -> x <> y.
|
||||||
|
Proof.
|
||||||
|
intros. assert (~ E.eq x y). auto using singleton_2.
|
||||||
|
intros J. subst. auto with *.
|
||||||
|
contradict H0.
|
||||||
|
rewrite H0.
|
||||||
|
apply E.eq_refl.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma notin_singleton_swap : forall x y,
|
||||||
|
~ In x (singleton y) -> ~ In y (singleton x).
|
||||||
|
Proof.
|
||||||
|
intros.
|
||||||
|
assert (Q := elim_notin_singleton H).
|
||||||
|
auto using singleton_1.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** ** Rewriting non-membership facts *)
|
||||||
|
|
||||||
|
Lemma notin_singleton_rw : forall x y,
|
||||||
|
~ In x (singleton y) <-> ~ E.eq x y.
|
||||||
|
Proof.
|
||||||
|
intros. split.
|
||||||
|
auto using elim_notin_singleton.
|
||||||
|
auto using notin_singleton.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** ** Tactics *)
|
||||||
|
|
||||||
|
(** The tactic [notin_simpl_hyps] destructs all hypotheses of the form
|
||||||
|
[(~ In x E)], where [E] is built using only [empty], [union], and
|
||||||
|
[singleton]. *)
|
||||||
|
|
||||||
|
Ltac notin_simpl_hyps :=
|
||||||
|
try match goal with
|
||||||
|
| H: In ?x ?E -> False |- _ =>
|
||||||
|
change (~ In x E) in H;
|
||||||
|
notin_simpl_hyps
|
||||||
|
| H: ~ In _ empty |- _ =>
|
||||||
|
clear H;
|
||||||
|
notin_simpl_hyps
|
||||||
|
| H: ~ In ?x (singleton ?y) |- _ =>
|
||||||
|
let F1 := fresh in
|
||||||
|
let F2 := fresh in
|
||||||
|
assert (F1 := @elim_notin_singleton x y H);
|
||||||
|
assert (F2 := @elim_notin_singleton' x y H);
|
||||||
|
clear H;
|
||||||
|
notin_simpl_hyps
|
||||||
|
| H: ~ In ?x (union ?E ?F) |- _ =>
|
||||||
|
destruct (@elim_notin_union x E F H);
|
||||||
|
clear H;
|
||||||
|
notin_simpl_hyps
|
||||||
|
end.
|
||||||
|
|
||||||
|
(** The tactic [notin_solve] solves goals of them form [(x <> y)] and
|
||||||
|
[(~ In x E)] that are provable from hypotheses of the form
|
||||||
|
destructed by [notin_simpl_hyps]. *)
|
||||||
|
|
||||||
|
Ltac notin_solve :=
|
||||||
|
notin_simpl_hyps;
|
||||||
|
repeat (progress ( apply notin_empty
|
||||||
|
|| apply notin_union
|
||||||
|
|| apply notin_singleton));
|
||||||
|
solve [ trivial | congruence | intuition auto ].
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** ** Examples and test cases *)
|
||||||
|
|
||||||
|
Lemma test_notin_solve_1 : forall x E F G,
|
||||||
|
~ In x (union E F) -> ~ In x G -> ~ In x (union E G).
|
||||||
|
Proof.
|
||||||
|
intros. notin_solve.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma test_notin_solve_2 : forall x y E F G,
|
||||||
|
~ In x (union E (union (singleton y) F)) -> ~ In x G ->
|
||||||
|
~ In x (singleton y) /\ ~ In y (singleton x).
|
||||||
|
Proof.
|
||||||
|
intros.
|
||||||
|
split.
|
||||||
|
notin_solve.
|
||||||
|
|
||||||
|
apply notin_singleton.
|
||||||
|
generalize H.
|
||||||
|
apply notin_union.
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma test_notin_solve_3 : forall x y,
|
||||||
|
~ E.eq x y -> ~ In x (singleton y) /\ ~ In y (singleton x).
|
||||||
|
Proof.
|
||||||
|
intros. split. notin_solve.
|
||||||
|
(* notin_solve.*)
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
Lemma test_notin_solve_4 : forall x y E F G,
|
||||||
|
~ In x (union E (union (singleton x) F)) -> ~ In y G.
|
||||||
|
Proof.
|
||||||
|
intros. notin_solve.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma test_notin_solve_5 : forall x y E F,
|
||||||
|
~ In x (union E (union (singleton y) F)) -> ~ In y E ->
|
||||||
|
~ E.eq y x /\ ~ E.eq x y.
|
||||||
|
Proof.
|
||||||
|
intros. split.
|
||||||
|
(* notin_solve. notin_solve.*)
|
||||||
|
Admitted.
|
||||||
|
|
||||||
|
End Notin.
|
||||||
493
share/popl08-tutorial-Fsub/Fsub_Definitions.v.crashcoqide
Normal file
|
|
@ -0,0 +1,493 @@
|
||||||
|
(** Definition of Fsub (System F with subtyping).
|
||||||
|
|
||||||
|
Authors: Brian Aydemir and Arthur Charguéraud, with help from
|
||||||
|
Aaron Bohannon, Jeffrey Vaughan, and Dimitrios Vytiniotis.
|
||||||
|
|
||||||
|
Table of contents:
|
||||||
|
- #<a href="##syntax">Syntax (pre-terms)</a>#
|
||||||
|
- #<a href="##open">Opening</a>#
|
||||||
|
- #<a href="##lc">Local closure</a>#
|
||||||
|
- #<a href="##env">Environments</a>#
|
||||||
|
- #<a href="##wf">Well-formedness</a>#
|
||||||
|
- #<a href="##sub">Subtyping</a>#
|
||||||
|
- #<a href="##typing_doc">Typing</a>#
|
||||||
|
- #<a href="##values">Values</a>#
|
||||||
|
- #<a href="##reduction">Reduction</a>#
|
||||||
|
- #<a href="##auto">Automation</a>#
|
||||||
|
*)
|
||||||
|
|
||||||
|
Require Export Metatheory.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="syntax"></a># Syntax (pre-terms) *)
|
||||||
|
|
||||||
|
(** We use a locally nameless representation for Fsub, where bound
|
||||||
|
variables are represented as natural numbers (de Bruijn indices)
|
||||||
|
and free variables are represented as [atom]s. The type [atom],
|
||||||
|
defined in the [Atom] library, represents names: there are
|
||||||
|
infinitely many atoms, equality is decidable on atoms, and it is
|
||||||
|
possible to generate an atom fresh for any given finite set of
|
||||||
|
atoms.
|
||||||
|
|
||||||
|
We say that the definitions below define pre-types ([typ]) and
|
||||||
|
pre-expressions ([exp]), collectively pre-terms, since the
|
||||||
|
datatypes admit terms, such as [(typ_all typ_top (typ_bvar 3))],
|
||||||
|
where indices are unbound. A term is locally closed when it
|
||||||
|
contains no unbound indices.
|
||||||
|
|
||||||
|
Note that indices for bound type variables are distinct from
|
||||||
|
indices for bound expression variables. We make this explicit in
|
||||||
|
the definitions below of the opening operations. *)
|
||||||
|
|
||||||
|
Inductive typ : Set :=
|
||||||
|
| typ_top : typ
|
||||||
|
| typ_bvar : nat -> typ
|
||||||
|
| typ_fvar : atom -> typ
|
||||||
|
| typ_arrow : typ -> typ -> typ
|
||||||
|
| typ_all : typ -> typ -> typ
|
||||||
|
.
|
||||||
|
|
||||||
|
Inductive exp : Set :=
|
||||||
|
| exp_bvar : nat -> exp
|
||||||
|
| exp_fvar : atom -> exp
|
||||||
|
| exp_abs : typ -> exp -> exp
|
||||||
|
| exp_app : exp -> exp -> exp
|
||||||
|
| exp_tabs : typ -> exp -> exp
|
||||||
|
| exp_tapp : exp -> typ -> exp
|
||||||
|
.
|
||||||
|
|
||||||
|
(** We declare the constructors for indices and variables to be
|
||||||
|
coercions. For example, if Coq sees a [nat] where it expects an
|
||||||
|
[exp], it will implicitly insert an application of [exp_bvar];
|
||||||
|
similar behavior happens for [atom]s. Thus, we may write
|
||||||
|
[(exp_abs typ_top (exp_app 0 x))] instead of [(exp_abs typ_top
|
||||||
|
(exp_app (exp_bvar 0) (exp_fvar x)))]. *)
|
||||||
|
|
||||||
|
Coercion typ_bvar : nat >-> typ.
|
||||||
|
Coercion typ_fvar : atom >-> typ.
|
||||||
|
Coercion exp_bvar : nat >-> exp.
|
||||||
|
Coercion exp_fvar : atom >-> exp.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="open"></a># Opening terms *)
|
||||||
|
|
||||||
|
(** Opening replaces an index with a term. This operation is required
|
||||||
|
if we wish to work only with locally closed terms when going under
|
||||||
|
binders (e.g., the typing rule for [exp_abs]). It also
|
||||||
|
corresponds to informal substitution for a bound variable, which
|
||||||
|
occurs in the rule for beta reduction.
|
||||||
|
|
||||||
|
We need to define three functions for opening due the syntax of
|
||||||
|
Fsub, and we name them according to the following convention.
|
||||||
|
- [tt]: Denotes an operation involving types appearing in types.
|
||||||
|
- [te]: Denotes an operation involving types appearing in
|
||||||
|
expressions.
|
||||||
|
- [ee]: Denotes an operation involving expressions appearing in
|
||||||
|
expressions.
|
||||||
|
|
||||||
|
The notation used below for decidable equality on atoms and
|
||||||
|
natural numbers (e.g., [K === J]) is defined in the [Metatheory]
|
||||||
|
library. The order of arguments to each "open" function is the
|
||||||
|
same. For example, [(open_tt_rec K U T)] can be read as
|
||||||
|
"substitute [U] for index [K] in [T]."
|
||||||
|
|
||||||
|
Note that we assume that [U] is locally closed (and similarly for
|
||||||
|
the other opening functions). This assumption simplifies the
|
||||||
|
implementations of opening by letting us avoid shifting. Since
|
||||||
|
bound variables are indices, there is no need to rename variables
|
||||||
|
to avoid capture. Finally, we assume that these functions are
|
||||||
|
initially called with index zero and that zero is the only unbound
|
||||||
|
index in the term. This eliminates the need to possibly subtract
|
||||||
|
one in the case of indices. *)
|
||||||
|
|
||||||
|
Fixpoint open_tt_rec (K : nat) (U : typ) (T : typ) {struct T} : typ :=
|
||||||
|
match T with
|
||||||
|
| typ_top => typ_top
|
||||||
|
| typ_bvar J => if K === J then U else (typ_bvar J)
|
||||||
|
| typ_fvar X => typ_fvar X
|
||||||
|
| typ_arrow T1 T2 => typ_arrow (open_tt_rec K U T1) (open_tt_rec K U T2)
|
||||||
|
| typ_all T1 T2 => typ_all (open_tt_rec K U T1) (open_tt_rec (S K) U T2)
|
||||||
|
end.
|
||||||
|
|
||||||
|
Fixpoint open_te_rec (K : nat) (U : typ) (e : exp) {struct e} : exp :=
|
||||||
|
match e with
|
||||||
|
| exp_bvar i => exp_bvar i
|
||||||
|
| exp_fvar x => exp_fvar x
|
||||||
|
| exp_abs V e1 => exp_abs (open_tt_rec K U V) (open_te_rec K U e1)
|
||||||
|
| exp_app e1 e2 => exp_app (open_te_rec K U e1) (open_te_rec K U e2)
|
||||||
|
| exp_tabs V e1 => exp_tabs (open_tt_rec K U V) (open_te_rec (S K) U e1)
|
||||||
|
| exp_tapp e1 V => exp_tapp (open_te_rec K U e1) (open_tt_rec K U V)
|
||||||
|
end.
|
||||||
|
|
||||||
|
Fixpoint open_ee_rec (k : nat) (f : exp) (e : exp) {struct e} : exp :=
|
||||||
|
match e with
|
||||||
|
| exp_bvar i => if k === i then f else (exp_bvar i)
|
||||||
|
| exp_fvar x => exp_fvar x
|
||||||
|
| exp_abs V e1 => exp_abs V (open_ee_rec (S k) f e1)
|
||||||
|
| exp_app e1 e2 => exp_app (open_ee_rec k f e1) (open_ee_rec k f e2)
|
||||||
|
| exp_tabs V e1 => exp_tabs V (open_ee_rec k f e1)
|
||||||
|
| exp_tapp e1 V => exp_tapp (open_ee_rec k f e1) V
|
||||||
|
end.
|
||||||
|
|
||||||
|
(** Many common applications of opening replace index zero with an
|
||||||
|
expression or variable. The following definitions provide
|
||||||
|
convenient shorthands for such uses. Note that the order of
|
||||||
|
arguments is switched relative to the definitions above. For
|
||||||
|
example, [(open_tt T X)] can be read as "substitute the variable
|
||||||
|
[X] for index [0] in [T]" and "open [T] with the variable [X]."
|
||||||
|
Recall that the coercions above let us write [X] in place of
|
||||||
|
[(typ_fvar X)], assuming that [X] is an [atom]. *)
|
||||||
|
|
||||||
|
Definition open_tt T U := open_tt_rec 0 U T.
|
||||||
|
Definition open_te e U := open_te_rec 0 U e.
|
||||||
|
Definition open_ee e1 e2 := open_ee_rec 0 e2 e1.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="lc"></a># Local closure *)
|
||||||
|
|
||||||
|
(** Recall that [typ] and [exp] define pre-terms; these datatypes
|
||||||
|
admit terms that contain unbound indices. A term is locally
|
||||||
|
closed, or syntactically well-formed, when no indices appearing in
|
||||||
|
it are unbound. The proposition [(type T)] holds when a type [T]
|
||||||
|
is locally closed, and [(expr e)] holds when an expression [e] is
|
||||||
|
locally closed.
|
||||||
|
|
||||||
|
The inductive definitions below formalize local closure such that
|
||||||
|
the resulting induction principles serve as structural induction
|
||||||
|
principles over (locally closed) types and (locally closed)
|
||||||
|
expressions. In particular, unlike the situation with pre-terms,
|
||||||
|
there are no cases for indices. Thus, these induction principles
|
||||||
|
correspond more closely to informal practice than the ones arising
|
||||||
|
from the definitions of pre-terms.
|
||||||
|
|
||||||
|
The interesting cases in the inductive definitions below are those
|
||||||
|
that involve binding constructs, e.g., [typ_all]. Intuitively, to
|
||||||
|
check if the pre-term [(typ_all T1 T2)] is locally closed we much
|
||||||
|
check that [T1] is locally closed, and that [T2] is locally closed
|
||||||
|
when opened with a variable. However, there is a choice as to how
|
||||||
|
many variables to quantify over. One possibility is to quantify
|
||||||
|
over only one variable ("existential" quantification), as in
|
||||||
|
<<
|
||||||
|
type_all : forall X T1 T2,
|
||||||
|
type T1 ->
|
||||||
|
type (open_tt T2 X) ->
|
||||||
|
type (typ_all T1 T2)
|
||||||
|
>> or we could quantify over as many variables as possible ("universal"
|
||||||
|
quantification), as in
|
||||||
|
<<
|
||||||
|
type_all : forall T1 T2,
|
||||||
|
type T1 ->
|
||||||
|
(forall X : atom, type (open_tt T2 X)) ->
|
||||||
|
type (typ_all T1 T2)
|
||||||
|
>> It is possible to show that the resulting relations are equivalent.
|
||||||
|
The former makes it easy to build derivations, while the latter
|
||||||
|
provides a strong induction principle. McKinna and Pollack used
|
||||||
|
both forms of this relation in their work on formalizing Pure Type
|
||||||
|
Systems.
|
||||||
|
|
||||||
|
We take a different approach here and use "cofinite
|
||||||
|
quantification": we quantify over all but finitely many variables.
|
||||||
|
This approach provides a convenient middle ground: we can build
|
||||||
|
derivations reasonably easily and get reasonably strong induction
|
||||||
|
principles. With some work, one can show that the definitions
|
||||||
|
below are equivalent to ones that use existential, and hence also
|
||||||
|
universal, quantification. *)
|
||||||
|
|
||||||
|
Inductive type : typ -> Prop :=
|
||||||
|
| type_top :
|
||||||
|
type typ_top
|
||||||
|
| type_var : forall X,
|
||||||
|
type (typ_fvar X)
|
||||||
|
| type_arrow : forall T1 T2,
|
||||||
|
type T1 ->
|
||||||
|
type T2 ->
|
||||||
|
type (typ_arrow T1 T2)
|
||||||
|
| type_all : forall L T1 T2,
|
||||||
|
type T1 ->
|
||||||
|
(forall X : atom, X `notin` L -> type (open_tt T2 X)) ->
|
||||||
|
type (typ_all T1 T2)
|
||||||
|
.
|
||||||
|
|
||||||
|
Inductive expr : exp -> Prop :=
|
||||||
|
| expr_var : forall x,
|
||||||
|
expr (exp_fvar x)
|
||||||
|
| expr_abs : forall L T e1,
|
||||||
|
type T ->
|
||||||
|
(forall x : atom, x `notin` L -> expr (open_ee e1 x)) ->
|
||||||
|
expr (exp_abs T e1)
|
||||||
|
| expr_app : forall e1 e2,
|
||||||
|
expr e1 ->
|
||||||
|
expr e2 ->
|
||||||
|
expr (exp_app e1 e2)
|
||||||
|
| expr_tabs : forall L T e1,
|
||||||
|
type T ->
|
||||||
|
(forall X : atom, X `notin` L -> expr (open_te e1 X)) ->
|
||||||
|
expr (exp_tabs T e1)
|
||||||
|
| expr_tapp : forall e1 V,
|
||||||
|
expr e1 ->
|
||||||
|
type V ->
|
||||||
|
expr (exp_tapp e1 V)
|
||||||
|
.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="env"></a># Environments *)
|
||||||
|
|
||||||
|
(** In our presentation of System F with subtyping, we use a single
|
||||||
|
environment for both typing and subtyping assumptions. We
|
||||||
|
formalize environments by representing them as association lists
|
||||||
|
(lists of pairs of keys and values) whose keys are atoms.
|
||||||
|
|
||||||
|
The [Metatheory] and [Environment] libraries provide functions,
|
||||||
|
predicates, tactics, notations and lemmas that simplify working
|
||||||
|
with environments. The [Environment] library treats environments
|
||||||
|
as lists of type [list (atom * A)].
|
||||||
|
|
||||||
|
Since environments map [atom]s, the type [A] should encode whether
|
||||||
|
a particular binding is a typing or subtyping assumption. Thus,
|
||||||
|
we instantiate [A] with the type [binding], defined below. *)
|
||||||
|
|
||||||
|
Inductive binding : Set :=
|
||||||
|
| bind_sub : typ -> binding
|
||||||
|
| bind_typ : typ -> binding.
|
||||||
|
|
||||||
|
(** A binding [(X, bind_sub T)] records that a type variable [X] is a
|
||||||
|
subtype of [T], and a binding [(x, bind_typ U)] records that an
|
||||||
|
expression variable [x] has type [U].
|
||||||
|
|
||||||
|
We define an abbreviation [env] for the type of environments, and
|
||||||
|
an abbreviation [empty] for the empty environment.
|
||||||
|
|
||||||
|
Note: Each instance of [Notation] below defines an abbreviation
|
||||||
|
since the left-hand side consists of a single identifier that is
|
||||||
|
not in quotes. These abbreviations are used for both parsing (the
|
||||||
|
left-hand side is equivalent to the right-hand side in all
|
||||||
|
contexts) and printing (the right-hand side is pretty-printed as
|
||||||
|
the left-hand side). Since [nil] is normally a polymorphic
|
||||||
|
constructor whose type argument is implicit, we prefix the name
|
||||||
|
with "[@]" to signal to Coq that we are going to supply arguments
|
||||||
|
to [nil] explicitly. *)
|
||||||
|
|
||||||
|
Notation env := (list (atom * binding)).
|
||||||
|
Notation empty := (@nil (atom * binding)).
|
||||||
|
|
||||||
|
(** We also define a notation that makes it convenient to write one
|
||||||
|
element lists. This notation is useful because of our convention
|
||||||
|
for building environments; see the examples below. *)
|
||||||
|
|
||||||
|
Notation "[ x ]" := (x :: nil).
|
||||||
|
|
||||||
|
(** #<b>#Examples:#</b># We use a convention where environments are
|
||||||
|
never built using a cons operation [((x, a) :: E)] where [E] is
|
||||||
|
non-[nil]. This makes the shape of environments more uniform and
|
||||||
|
saves us from excessive fiddling with the shapes of environments.
|
||||||
|
For example, Coq's tactics sometimes distinguish between consing
|
||||||
|
on a new binding and prepending a one element list, even though
|
||||||
|
the two operations are convertible with each other.
|
||||||
|
|
||||||
|
Consider the following environments written in informal notation.
|
||||||
|
<<
|
||||||
|
1. (empty environment)
|
||||||
|
2. x : T
|
||||||
|
3. x : T, Y <: S
|
||||||
|
4. E, x : T, F
|
||||||
|
>> In the third example, we have an environment that binds an
|
||||||
|
expression variable [x] to [T] and a type variable [Y] to [S].
|
||||||
|
In Coq, we would write these environments as follows.
|
||||||
|
<<
|
||||||
|
1. empty
|
||||||
|
2. [(x, bind_typ T)]
|
||||||
|
3. [(Y, bind_sub S)] ++ [(x, bind_typ T)]
|
||||||
|
4. F ++ [(x, bind_typ T)] ++ E
|
||||||
|
>> The symbol "[++]" denotes list concatenation and associates to the
|
||||||
|
right. (That notation is defined in Coq's [List] library.) Note
|
||||||
|
that in Coq, environments grow on the left, since that is where
|
||||||
|
the head of a list is. *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="wf"></a># Well-formedness *)
|
||||||
|
|
||||||
|
(** A type [T] is well-formed with respect to an environment [E],
|
||||||
|
denoted [(wf_typ E T)], when [T] is locally-closed and its free
|
||||||
|
variables are bound in [E]. We need this relation in order to
|
||||||
|
restrict the subtyping and typing relations, defined below, to
|
||||||
|
contain only well-formed types. (This relation is missing in the
|
||||||
|
original statement of the POPLmark Challenge.)
|
||||||
|
|
||||||
|
Note: It is tempting to define the premise of [wf_typ_var] as [(X
|
||||||
|
`in` dom E)], since that makes the rule easier to apply (no need
|
||||||
|
to guess an instantiation for [U]). Unfortunately, this is
|
||||||
|
incorrect. We need to check that [X] is bound as a type-variable,
|
||||||
|
not an expression-variable; [(dom E)] does not distinguish between
|
||||||
|
the two kinds of bindings. *)
|
||||||
|
|
||||||
|
Inductive wf_typ : env -> typ -> Prop :=
|
||||||
|
| wf_typ_top : forall E,
|
||||||
|
wf_typ E typ_top
|
||||||
|
| wf_typ_var : forall U E (X : atom),
|
||||||
|
binds X (bind_sub U) E ->
|
||||||
|
wf_typ E (typ_fvar X)
|
||||||
|
| wf_typ_arrow : forall E T1 T2,
|
||||||
|
wf_typ E T1 ->
|
||||||
|
wf_typ E T2 ->
|
||||||
|
wf_typ E (typ_arrow T1 T2)
|
||||||
|
| wf_typ_all : forall L E T1 T2,
|
||||||
|
wf_typ E T1 ->
|
||||||
|
(forall X : atom, X `notin` L ->
|
||||||
|
wf_typ ([(X, bind_sub T1)] ++ E) (open_tt T2 X)) ->
|
||||||
|
wf_typ E (typ_all T1 T2)
|
||||||
|
.
|
||||||
|
|
||||||
|
(** An environment E is well-formed, denoted [(wf_env E)], if each
|
||||||
|
atom is bound at most at once and if each binding is to a
|
||||||
|
well-formed type. This is a stronger relation than the [ok]
|
||||||
|
relation defined in the [Environment] library. We need this
|
||||||
|
relation in order to restrict the subtyping and typing relations,
|
||||||
|
defined below, to contain only well-formed environments. (This
|
||||||
|
relation is missing in the original statement of the POPLmark
|
||||||
|
Challenge.) *)
|
||||||
|
|
||||||
|
Inductive wf_env : env -> Prop :=
|
||||||
|
| wf_env_empty :
|
||||||
|
wf_env empty
|
||||||
|
| wf_env_sub : forall (E : env) (X : atom) (T : typ),
|
||||||
|
wf_env E ->
|
||||||
|
wf_typ E T ->
|
||||||
|
X `notin` dom E ->
|
||||||
|
wf_env ([(X, bind_sub T)] ++ E)
|
||||||
|
| wf_env_typ : forall (E : env) (x : atom) (T : typ),
|
||||||
|
wf_env E ->
|
||||||
|
wf_typ E T ->
|
||||||
|
x `notin` dom E ->
|
||||||
|
wf_env ([(x, bind_typ T)] ++ E).
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="sub"></a># Subtyping *)
|
||||||
|
|
||||||
|
(** The definition of subtyping is straightforward. It uses the
|
||||||
|
[binds] relation from the [Environment] library (in the
|
||||||
|
[sub_trans_tvar] case) and cofinite quantification (in the
|
||||||
|
[sub_all] case). *)
|
||||||
|
|
||||||
|
Inductive sub : env -> typ -> typ -> Prop :=
|
||||||
|
| sub_top : forall E S,
|
||||||
|
wf_env E ->
|
||||||
|
wf_typ E S ->
|
||||||
|
sub E S typ_top
|
||||||
|
| sub_refl_tvar : forall E X,
|
||||||
|
wf_env E ->
|
||||||
|
wf_typ E (typ_fvar X) ->
|
||||||
|
sub E (typ_fvar X) (typ_fvar X)
|
||||||
|
| sub_trans_tvar : forall U E T X,
|
||||||
|
binds X (bind_sub U) E ->
|
||||||
|
sub E U T ->
|
||||||
|
sub E (typ_fvar X) T
|
||||||
|
| sub_arrow : forall E S1 S2 T1 T2,
|
||||||
|
sub E T1 S1 ->
|
||||||
|
sub E S2 T2 ->
|
||||||
|
sub E (typ_arrow S1 S2) (typ_arrow T1 T2)
|
||||||
|
| sub_all : forall L E S1 S2 T1 T2,
|
||||||
|
sub E T1 S1 ->
|
||||||
|
(forall X : atom, X `notin` L ->
|
||||||
|
sub ([(X, bind_sub T1)] ++ E) (open_tt S2 X) (open_tt T2 X)) ->
|
||||||
|
sub E (typ_all S1 S2) (typ_all T1 T2)
|
||||||
|
.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="typing_doc"></a># Typing *)
|
||||||
|
|
||||||
|
(** The definition of typing is straightforward. It uses the [binds]
|
||||||
|
relation from the [Environment] library (in the [typing_var] case)
|
||||||
|
and cofinite quantification in the cases involving binders (e.g.,
|
||||||
|
[typing_abs] and [typing_tabs]). *)
|
||||||
|
|
||||||
|
Inductive typing : env -> exp -> typ -> Prop :=
|
||||||
|
| typing_var : forall E x T,
|
||||||
|
wf_env E ->
|
||||||
|
binds x (bind_typ T) E ->
|
||||||
|
typing E (exp_fvar x) T
|
||||||
|
| typing_abs : forall L E V e1 T1,
|
||||||
|
(forall x : atom, x `notin` L ->
|
||||||
|
typing ([(x, bind_typ V)] ++ E) (open_ee e1 x) T1) ->
|
||||||
|
typing E (exp_abs V e1) (typ_arrow V T1)
|
||||||
|
| typing_app : forall T1 E e1 e2 T2,
|
||||||
|
typing E e1 (typ_arrow T1 T2) ->
|
||||||
|
typing E e2 T1 ->
|
||||||
|
typing E (exp_app e1 e2) T2
|
||||||
|
| typing_tabs : forall L E V e1 T1,
|
||||||
|
(forall X : atom, X `notin` L ->
|
||||||
|
typing ([(X, bind_sub V)] ++ E) (open_te e1 X) (open_tt T1 X)) ->
|
||||||
|
typing E (exp_tabs V e1) (typ_all V T1)
|
||||||
|
| typing_tapp : forall T1 E e1 T T2,
|
||||||
|
typing E e1 (typ_all T1 T2) ->
|
||||||
|
sub E T T1 ->
|
||||||
|
typing E (exp_tapp e1 T) (open_tt T2 T)
|
||||||
|
| typing_sub : forall S E e T,
|
||||||
|
typing E e S ->
|
||||||
|
sub E S T ->
|
||||||
|
typing E e T
|
||||||
|
.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="values"></a># Values *)
|
||||||
|
|
||||||
|
Inductive value : exp -> Prop :=
|
||||||
|
| value_abs : forall T e1,
|
||||||
|
expr (exp_abs T e1) ->
|
||||||
|
value (exp_abs T e1)
|
||||||
|
| value_tabs : forall T e1,
|
||||||
|
expr (exp_tabs T e1) ->
|
||||||
|
value (exp_tabs T e1)
|
||||||
|
.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="reduction"></a># Reduction *)
|
||||||
|
|
||||||
|
Inductive red : exp -> exp -> Prop :=
|
||||||
|
| red_app_1 : forall e1 e1' e2,
|
||||||
|
expr e2 ->
|
||||||
|
red e1 e1' ->
|
||||||
|
red (exp_app e1 e2) (exp_app e1' e2)
|
||||||
|
| red_app_2 : forall e1 e2 e2',
|
||||||
|
value e1 ->
|
||||||
|
red e2 e2' ->
|
||||||
|
red (exp_app e1 e2) (exp_app e1 e2')
|
||||||
|
| red_tapp : forall e1 e1' V,
|
||||||
|
type V ->
|
||||||
|
red e1 e1' ->
|
||||||
|
red (exp_tapp e1 V) (exp_tapp e1' V)
|
||||||
|
| red_abs : forall T e1 v2,
|
||||||
|
expr (exp_abs T e1) ->
|
||||||
|
value v2 ->
|
||||||
|
red (exp_app (exp_abs T e1) v2) (open_ee e1 v2)
|
||||||
|
| red_tabs : forall T1 e1 T2,
|
||||||
|
expr (exp_tabs T1 e1) ->
|
||||||
|
type T2 ->
|
||||||
|
red (exp_tapp (exp_tabs T1 e1) T2) (open_te e1 T2)
|
||||||
|
.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="auto"></a># Automation *)
|
||||||
|
|
||||||
|
(** We declare most constructors as [Hint]s to be used by the [auto]
|
||||||
|
and [eauto] tactics. We exclude constructors from the subtyping
|
||||||
|
and typing relations that use cofinite quantification. It is
|
||||||
|
unlikely that [eauto] will find an instantiation for the finite
|
||||||
|
set [L], and in those cases, [eauto] can take some time to fail.
|
||||||
|
(A priori, this is not obvious. In practice, one adds as hints
|
||||||
|
all constructors and then later removes some constructors when
|
||||||
|
they cause proof search to take too long.) *)
|
||||||
|
|
||||||
|
Hint Constructors type expr wf_typ wf_env value red.
|
||||||
|
Hint Resolve sub_top sub_refl_tvar sub_arrow.
|
||||||
|
Hint Resolve typing_var typing_app typing_tapp typing_sub.
|
||||||
408
share/popl08-tutorial-Fsub/Fsub_Lemmas.v.crashcoqide
Normal file
|
|
@ -0,0 +1,408 @@
|
||||||
|
(** Administrative lemmas for Fsub.
|
||||||
|
|
||||||
|
Authors: Brian Aydemir and Arthur Charguéraud, with help from
|
||||||
|
Aaron Bohannon, Jeffrey Vaughan, and Dimitrios Vytiniotis.
|
||||||
|
|
||||||
|
This file contains a number of administrative lemmas that we
|
||||||
|
require for proving type-safety. The lemmas mainly concern the
|
||||||
|
relations [wf_typ] and [wf_env].
|
||||||
|
|
||||||
|
This file also contains regularity lemmas, which show that various
|
||||||
|
relations hold only for locally closed terms. In addition to
|
||||||
|
being necessary to complete the proof of type-safety, these lemmas
|
||||||
|
help demonstrate that our definitions are correct; they would be
|
||||||
|
worth proving even if they are unneeded for any "real" proofs.
|
||||||
|
|
||||||
|
Table of contents:
|
||||||
|
- #<a href="##wft">Properties of wf_typ</a>#
|
||||||
|
- #<a href="##oktwft">Properties of wf_env and wf_typ</a>#
|
||||||
|
- #<a href="##okt">Properties of wf_env</a>#
|
||||||
|
- #<a href="##subst">Properties of substitution</a>#
|
||||||
|
- #<a href="##regularity">Regularity lemmas</a>#
|
||||||
|
- #<a href="##auto">Automation</a># *)
|
||||||
|
|
||||||
|
Require Import Coq.Lists.List.
|
||||||
|
Include ListNotations.
|
||||||
|
|
||||||
|
Require Import Fsub_Infrastructure.
|
||||||
|
Require Import AdditionalTactics.
|
||||||
|
Include AdditionalTactics.
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="wft"></a># Properties of [wf_typ] *)
|
||||||
|
|
||||||
|
(** If a type is well-formed in an environment, then it is locally
|
||||||
|
closed. *)
|
||||||
|
|
||||||
|
Lemma type_from_wf_typ : forall E T,
|
||||||
|
wf_typ E T -> type T.
|
||||||
|
Proof.
|
||||||
|
intros E T H; induction H; eauto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** The remaining properties are analogous to the properties that we
|
||||||
|
need to show for the subtyping and typing relations. *)
|
||||||
|
|
||||||
|
Lemma wf_typ_weakening : forall T E F G,
|
||||||
|
wf_typ (G ++ E) T ->
|
||||||
|
ok (G ++ F ++ E) ->
|
||||||
|
wf_typ (G ++ F ++ E) T.
|
||||||
|
Proof with simpl_env; eauto.
|
||||||
|
intros T E F G Hwf_typ Hk.
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
remember (G ++ E) as F in |-.
|
||||||
|
generalize dependent G.
|
||||||
|
induction Hwf_typ; intros G Hok Heq; subst...
|
||||||
|
Case "type_all".
|
||||||
|
pick fresh Y and apply wf_typ_all...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.*)
|
||||||
|
|
||||||
|
Lemma wf_typ_weaken_head : forall T (E:env) (F:env),
|
||||||
|
wf_typ E T ->
|
||||||
|
ok (F ++ E) ->
|
||||||
|
wf_typ (F ++ E) T.
|
||||||
|
Proof.
|
||||||
|
intros.
|
||||||
|
Admitted.
|
||||||
|
(*
|
||||||
|
rewrite_env (empty ++ F++ E).
|
||||||
|
auto using wf_typ_weakening.
|
||||||
|
Qed.
|
||||||
|
*)
|
||||||
|
|
||||||
|
Lemma wf_typ_narrowing : forall V U T E F X,
|
||||||
|
wf_typ (F ++ [(X, bind_sub V)] ++ E) T ->
|
||||||
|
ok (F ++ [(X, bind_sub U)] ++ E) ->
|
||||||
|
wf_typ (F ++ [(X, bind_sub U)] ++ E) T.
|
||||||
|
Proof with simpl_env; eauto.
|
||||||
|
intros V U T E F X Hwf_typ Hok.
|
||||||
|
remember (F ++ [(X, bind_sub V)] ++ E) as G.
|
||||||
|
generalize dependent F.
|
||||||
|
induction Hwf_typ; intros F Hok Heq; subst...
|
||||||
|
Case "wf_typ_var".
|
||||||
|
binds_cases H...
|
||||||
|
Case "typ_all".
|
||||||
|
pick fresh Y and apply wf_typ_all...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_typ_strengthening : forall E F x U T,
|
||||||
|
wf_typ (F ++ [(x, bind_typ U)] ++ E) T ->
|
||||||
|
wf_typ (F ++ E) T.
|
||||||
|
Proof with simpl_env; eauto.
|
||||||
|
intros E F x U T H.
|
||||||
|
remember (F ++ [(x, bind_typ U)] ++ E) as G.
|
||||||
|
generalize dependent F.
|
||||||
|
induction H; intros F Heq; subst...
|
||||||
|
Case "wf_typ_var".
|
||||||
|
binds_cases H...
|
||||||
|
Case "wf_typ_all".
|
||||||
|
pick fresh Y and apply wf_typ_all...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H1...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_typ_subst_tb : forall F Q E Z P T,
|
||||||
|
wf_typ (F ++ [(Z, bind_sub Q)] ++ E) T ->
|
||||||
|
wf_typ E P ->
|
||||||
|
ok (map (subst_tb Z P) F ++ E) ->
|
||||||
|
wf_typ (map (subst_tb Z P) F ++ E) (subst_tt Z P T).
|
||||||
|
Proof with simpl_env; eauto using wf_typ_weaken_head, type_from_wf_typ.
|
||||||
|
intros F Q E Z P T WT WP.
|
||||||
|
remember (F ++ [(Z, bind_sub Q)] ++ E) as G.
|
||||||
|
generalize dependent F.
|
||||||
|
induction WT; intros F EQ Ok; subst; simpl subst_tt...
|
||||||
|
Case "wf_typ_var".
|
||||||
|
destruct (X == Z); subst...
|
||||||
|
SCase "X <> Z".
|
||||||
|
binds_cases H...
|
||||||
|
apply (wf_typ_var (subst_tt Z P U))...
|
||||||
|
Case "wf_typ_all".
|
||||||
|
pick fresh Y and apply wf_typ_all...
|
||||||
|
rewrite subst_tt_open_tt_var...
|
||||||
|
rewrite_env (map (subst_tb Z P) ([(Y, bind_sub T1)] ++ F) ++ E).
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_typ_open : forall E U T1 T2,
|
||||||
|
ok E ->
|
||||||
|
wf_typ E (typ_all T1 T2) ->
|
||||||
|
wf_typ E U ->
|
||||||
|
wf_typ E (open_tt T2 U).
|
||||||
|
Proof with simpl_env; eauto.
|
||||||
|
intros E U T1 T2 Ok WA WU.
|
||||||
|
inversion WA; subst.
|
||||||
|
pick fresh X.
|
||||||
|
rewrite (subst_tt_intro X)...
|
||||||
|
rewrite_env (map (subst_tb X U) empty ++ E).
|
||||||
|
eapply wf_typ_subst_tb...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="oktwft"></a># Properties of [wf_env] and [wf_typ] *)
|
||||||
|
|
||||||
|
Lemma ok_from_wf_env : forall E,
|
||||||
|
wf_env E ->
|
||||||
|
ok E.
|
||||||
|
Proof.
|
||||||
|
intros E H; induction H; auto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
(** We add [ok_from_wf_env] as a hint here since it helps blur the
|
||||||
|
distinction between [wf_env] and [ok] in proofs. The lemmas in
|
||||||
|
the [Environment] library use [ok], whereas here we naturally have
|
||||||
|
(or can easily show) the stronger [wf_env]. Thus,
|
||||||
|
[ok_from_wf_env] serves as a bridge that allows us to use the
|
||||||
|
environments library. *)
|
||||||
|
|
||||||
|
Hint Resolve ok_from_wf_env.
|
||||||
|
|
||||||
|
Lemma wf_typ_from_binds_typ : forall x U E,
|
||||||
|
wf_env E ->
|
||||||
|
binds x (bind_typ U) E ->
|
||||||
|
wf_typ E U.
|
||||||
|
Proof with auto using wf_typ_weaken_head.
|
||||||
|
induction 1; intros J; binds_cases J...
|
||||||
|
inversion H4; subst...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_typ_from_wf_env_typ : forall x T E,
|
||||||
|
wf_env ([(x, bind_typ T)] ++ E) ->
|
||||||
|
wf_typ E T.
|
||||||
|
Proof.
|
||||||
|
intros x T E H. inversion H; auto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_typ_from_wf_env_sub : forall x T E,
|
||||||
|
wf_env ([(x, bind_sub T)] ++ E) ->
|
||||||
|
wf_typ E T.
|
||||||
|
Proof.
|
||||||
|
intros x T E H. inversion H; auto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="okt"></a># Properties of [wf_env] *)
|
||||||
|
|
||||||
|
(** These properties are analogous to the properties that we need to
|
||||||
|
show for the subtyping and typing relations. *)
|
||||||
|
|
||||||
|
Lemma wf_env_narrowing : forall V E F U X,
|
||||||
|
wf_env (F ++ [(X, bind_sub V)] ++ E) ->
|
||||||
|
wf_typ E U ->
|
||||||
|
wf_env (F ++ [(X, bind_sub U)] ++ E).
|
||||||
|
Proof with eauto 6 using wf_typ_narrowing.
|
||||||
|
induction F; intros U X Wf_env Wf;
|
||||||
|
inversion Wf_env; subst; simpl_env in *...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_env_strengthening : forall x T E F,
|
||||||
|
wf_env (F ++ [(x, bind_typ T)] ++ E) ->
|
||||||
|
wf_env (F ++ E).
|
||||||
|
Proof with eauto using wf_typ_strengthening.
|
||||||
|
induction F; intros Wf_env; inversion Wf_env; subst; simpl_env in *...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma wf_env_subst_tb : forall Q Z P E F,
|
||||||
|
wf_env (F ++ [(Z, bind_sub Q)] ++ E) ->
|
||||||
|
wf_typ E P ->
|
||||||
|
wf_env (map (subst_tb Z P) F ++ E).
|
||||||
|
Proof with eauto 6 using wf_typ_subst_tb.
|
||||||
|
induction F; intros Wf_env WP; simpl_env;
|
||||||
|
inversion Wf_env; simpl_env in *; simpl subst_tb...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="subst"></a># Environment is unchanged by substitution for a fresh name *)
|
||||||
|
|
||||||
|
Lemma notin_fv_tt_open : forall (Y X : atom) T,
|
||||||
|
X `notin` fv_tt (open_tt T Y) ->
|
||||||
|
X `notin` fv_tt T.
|
||||||
|
Proof.
|
||||||
|
intros Y X T. unfold open_tt.
|
||||||
|
generalize 0.
|
||||||
|
induction T; simpl; intros k Fr; notin_simpl; try apply notin_union; eauto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma notin_fv_wf : forall E (X : atom) T,
|
||||||
|
wf_typ E T ->
|
||||||
|
X `notin` dom E ->
|
||||||
|
X `notin` fv_tt T.
|
||||||
|
Proof with auto.
|
||||||
|
intros E X T Wf_typ.
|
||||||
|
induction Wf_typ; intros Fr; simpl...
|
||||||
|
Case "wf_typ_var".
|
||||||
|
assert (X0 `in` (dom E))...
|
||||||
|
eapply binds_In; eauto.
|
||||||
|
Case "wf_typ_all".
|
||||||
|
apply notin_union...
|
||||||
|
pick fresh Y.
|
||||||
|
apply (notin_fv_tt_open Y)...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma map_subst_tb_id : forall G Z P,
|
||||||
|
wf_env G ->
|
||||||
|
Z `notin` dom G ->
|
||||||
|
G = map (subst_tb Z P) G.
|
||||||
|
Proof with auto.
|
||||||
|
intros G Z P H.
|
||||||
|
induction H; simpl; intros Fr; simpl_env...
|
||||||
|
rewrite <- IHwf_env...
|
||||||
|
rewrite <- subst_tt_fresh... eapply notin_fv_wf; eauto.
|
||||||
|
rewrite <- IHwf_env...
|
||||||
|
rewrite <- subst_tt_fresh... eapply notin_fv_wf; eauto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="regularity"></a># Regularity of relations *)
|
||||||
|
|
||||||
|
Lemma sub_regular : forall E S T,
|
||||||
|
sub E S T ->
|
||||||
|
wf_env E /\ wf_typ E S /\ wf_typ E T.
|
||||||
|
Proof with simpl_env; auto*.
|
||||||
|
intros E S T H.
|
||||||
|
induction H...
|
||||||
|
Case "sub_trans_tvar".
|
||||||
|
eauto*.
|
||||||
|
Case "sub_all".
|
||||||
|
repeat split...
|
||||||
|
SCase "Second of original three conjuncts".
|
||||||
|
pick fresh Y and apply wf_typ_all...
|
||||||
|
destruct (H1 Y)...
|
||||||
|
rewrite_env (empty ++ [(Y, bind_sub S1)] ++ E).
|
||||||
|
apply (wf_typ_narrowing T1)...
|
||||||
|
SCase "Third of original three conjuncts".
|
||||||
|
pick fresh Y and apply wf_typ_all...
|
||||||
|
destruct (H1 Y)...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma typing_regular : forall E e T,
|
||||||
|
typing E e T ->
|
||||||
|
wf_env E /\ expr e /\ wf_typ E T.
|
||||||
|
Proof with simpl_env; auto*.
|
||||||
|
intros E e T H; induction H...
|
||||||
|
Case "typing_var".
|
||||||
|
repeat split...
|
||||||
|
eauto using wf_typ_from_binds_typ.
|
||||||
|
Case "typing_abs".
|
||||||
|
pick fresh y.
|
||||||
|
destruct (H0 y) as [Hok [J K]]...
|
||||||
|
repeat split. inversion Hok...
|
||||||
|
SCase "Second of original three conjuncts".
|
||||||
|
pick fresh x and apply expr_abs.
|
||||||
|
eauto using type_from_wf_typ, wf_typ_from_wf_env_typ.
|
||||||
|
destruct (H0 x)...
|
||||||
|
SCase "Third of original three conjuncts".
|
||||||
|
apply wf_typ_arrow; eauto using wf_typ_from_wf_env_typ.
|
||||||
|
rewrite_env (empty ++ E).
|
||||||
|
eapply wf_typ_strengthening; simpl_env; eauto.
|
||||||
|
Case "typing_app".
|
||||||
|
repeat split...
|
||||||
|
destruct IHtyping1 as [_ [_ K]].
|
||||||
|
inversion K...
|
||||||
|
Case "typing_tabs".
|
||||||
|
pick fresh Y.
|
||||||
|
destruct (H0 Y) as [Hok [J K]]...
|
||||||
|
inversion Hok; subst.
|
||||||
|
repeat split...
|
||||||
|
SCase "Second of original three conjuncts".
|
||||||
|
pick fresh X and apply expr_tabs.
|
||||||
|
eauto using type_from_wf_typ, wf_typ_from_wf_env_sub...
|
||||||
|
destruct (H0 X)...
|
||||||
|
SCase "Third of original three conjuncts".
|
||||||
|
pick fresh Z and apply wf_typ_all...
|
||||||
|
destruct (H0 Z)...
|
||||||
|
Case "typing_tapp".
|
||||||
|
destruct (sub_regular _ _ _ H0) as [R1 [R2 R3]].
|
||||||
|
repeat split...
|
||||||
|
SCase "Second of original three conjuncts".
|
||||||
|
apply expr_tapp...
|
||||||
|
eauto using type_from_wf_typ.
|
||||||
|
SCase "Third of original three conjuncts".
|
||||||
|
destruct IHtyping as [R1' [R2' R3']].
|
||||||
|
eapply wf_typ_open; eauto.
|
||||||
|
Case "typing_sub".
|
||||||
|
repeat split...
|
||||||
|
destruct (sub_regular _ _ _ H0)...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma value_regular : forall e,
|
||||||
|
value e ->
|
||||||
|
expr e.
|
||||||
|
Proof.
|
||||||
|
intros e H. induction H; auto.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma red_regular : forall e e',
|
||||||
|
red e e' ->
|
||||||
|
expr e /\ expr e'.
|
||||||
|
Proof with auto*.
|
||||||
|
intros e e' H.
|
||||||
|
induction H; assert(J := value_regular); split...
|
||||||
|
Case "red_abs".
|
||||||
|
inversion H. pick fresh y. rewrite (subst_ee_intro y)...
|
||||||
|
Case "red_tabs".
|
||||||
|
inversion H. pick fresh Y. rewrite (subst_te_intro Y)...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* *********************************************************************** *)
|
||||||
|
(** * #<a name="auto"></a># Automation *)
|
||||||
|
|
||||||
|
(** The lemma [ok_from_wf_env] was already added above as a hint since it
|
||||||
|
helps blur the distinction between [wf_env] and [ok] in proofs.
|
||||||
|
|
||||||
|
As currently stated, the regularity lemmas are ill-suited to be
|
||||||
|
used with [auto] and [eauto] since they end in conjunctions. Even
|
||||||
|
if we were, for example, to split [sub_regularity] into three
|
||||||
|
separate lemmas, the resulting lemmas would be usable only by
|
||||||
|
[eauto] and there is no guarantee that [eauto] would be able to
|
||||||
|
find proofs effectively. Thus, the hints below apply the
|
||||||
|
regularity lemmas and [type_from_wf_typ] to discharge goals about
|
||||||
|
local closure and well-formedness, but in such a way as to
|
||||||
|
minimize proof search.
|
||||||
|
|
||||||
|
The first hint introduces an [wf_env] fact into the context. It
|
||||||
|
works well when combined with the lemmas relating [wf_env] and
|
||||||
|
[wf_typ]. We choose to use those lemmas explicitly via [(auto
|
||||||
|
using ...)] tactics rather than add them as hints. When used this
|
||||||
|
way, the explicitness makes the proof more informative rather than
|
||||||
|
more cluttered (with useless details).
|
||||||
|
|
||||||
|
The other three hints try outright to solve their respective
|
||||||
|
goals. *)
|
||||||
|
|
||||||
|
Hint Extern 1 (wf_env ?E) =>
|
||||||
|
match goal with
|
||||||
|
| H: sub _ _ _ |- _ => apply (proj1 (sub_regular _ _ _ H))
|
||||||
|
| H: typing _ _ _ |- _ => apply (proj1 (typing_regular _ _ _ H))
|
||||||
|
end.
|
||||||
|
|
||||||
|
Hint Extern 1 (wf_typ ?E ?T) =>
|
||||||
|
match goal with
|
||||||
|
| H: typing E _ T |- _ => apply (proj2 (proj2 (typing_regular _ _ _ H)))
|
||||||
|
| H: sub E T _ |- _ => apply (proj1 (proj2 (sub_regular _ _ _ H)))
|
||||||
|
| H: sub E _ T |- _ => apply (proj2 (proj2 (sub_regular _ _ _ H)))
|
||||||
|
end.
|
||||||
|
|
||||||
|
Hint Extern 1 (type ?T) =>
|
||||||
|
let go E := apply (type_from_wf_typ E); auto in
|
||||||
|
match goal with
|
||||||
|
| H: typing ?E _ T |- _ => go E
|
||||||
|
| H: sub ?E T _ |- _ => go E
|
||||||
|
| H: sub ?E _ T |- _ => go E
|
||||||
|
end.
|
||||||
|
|
||||||
|
Hint Extern 1 (expr ?e) =>
|
||||||
|
match goal with
|
||||||
|
| H: typing _ ?e _ |- _ => apply (proj1 (proj2 (typing_regular _ _ _ H)))
|
||||||
|
| H: red ?e _ |- _ => apply (proj1 (red_regular _ _ H))
|
||||||
|
| H: red _ ?e |- _ => apply (proj2 (red_regular _ _ H))
|
||||||
|
end.
|
||||||
593
share/popl08-tutorial-Fsub/Fsub_Soundness.v.crashcoqide
Normal file
|
|
@ -0,0 +1,593 @@
|
||||||
|
(** Type-safety proofs for Fsub.
|
||||||
|
|
||||||
|
Authors: Brian Aydemir and Arthur Charguéraud, with help from
|
||||||
|
Aaron Bohannon, Jeffrey Vaughan, and Dimitrios Vytiniotis.
|
||||||
|
|
||||||
|
In parentheses are given the label of the corresponding lemma in
|
||||||
|
the appendix (informal proofs) of the POPLmark Challenge.
|
||||||
|
|
||||||
|
Table of contents:
|
||||||
|
- #<a href="##subtyping">Properties of subtyping</a>#
|
||||||
|
- #<a href="##typing">Properties of typing</a>#
|
||||||
|
- #<a href="##preservation">Preservation</a>#
|
||||||
|
- #<a href="##progress">Progress</a># *)
|
||||||
|
|
||||||
|
Require Export Fsub_Lemmas.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="subtyping"></a># Properties of subtyping *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Reflexivity (1) *)
|
||||||
|
|
||||||
|
Lemma sub_reflexivity : forall E T,
|
||||||
|
wf_env E ->
|
||||||
|
wf_typ E T ->
|
||||||
|
sub E T T.
|
||||||
|
Proof with eauto.
|
||||||
|
intros E T Ok Wf.
|
||||||
|
induction Wf...
|
||||||
|
pick fresh Y and apply sub_all...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Weakening (2) *)
|
||||||
|
|
||||||
|
Lemma sub_weakening : forall E F G S T,
|
||||||
|
sub (G ++ E) S T ->
|
||||||
|
wf_env (G ++ F ++ E) ->
|
||||||
|
sub (G ++ F ++ E) S T.
|
||||||
|
Proof with simpl_env; auto using wf_typ_weakening.
|
||||||
|
intros E F G S T Sub Ok.
|
||||||
|
remember (G ++ E) as H.
|
||||||
|
generalize dependent G.
|
||||||
|
induction Sub; intros G Ok EQ; subst...
|
||||||
|
Case "sub_trans_tvar".
|
||||||
|
apply (sub_trans_tvar U)...
|
||||||
|
Case "sub_all".
|
||||||
|
pick fresh Y and apply sub_all...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Narrowing and transitivity (3) *)
|
||||||
|
|
||||||
|
Definition transitivity_on Q := forall E S T,
|
||||||
|
sub E S Q -> sub E Q T -> sub E S T.
|
||||||
|
|
||||||
|
Lemma sub_narrowing_aux : forall Q F E Z P S T,
|
||||||
|
transitivity_on Q ->
|
||||||
|
sub (F ++ [(Z, bind_sub Q)] ++ E) S T ->
|
||||||
|
sub E P Q ->
|
||||||
|
sub (F ++ [(Z, bind_sub P)] ++ E) S T.
|
||||||
|
Proof with simpl_env; eauto using wf_typ_narrowing, wf_env_narrowing.
|
||||||
|
intros Q F E Z P S T TransQ SsubT PsubQ.
|
||||||
|
remember (F ++ [(Z, bind_sub Q)] ++ E) as G. generalize dependent F.
|
||||||
|
induction SsubT; intros F EQ; subst...
|
||||||
|
Case "sub_top".
|
||||||
|
apply sub_top...
|
||||||
|
Case "sub_refl_tvar".
|
||||||
|
apply sub_refl_tvar...
|
||||||
|
Case "sub_trans_tvar".
|
||||||
|
destruct (X == Z); subst.
|
||||||
|
SCase "X = Z".
|
||||||
|
apply (sub_trans_tvar P); [ eauto using fresh_mid_head | ].
|
||||||
|
apply TransQ.
|
||||||
|
SSCase "P <: Q".
|
||||||
|
rewrite_env (empty ++ (F ++ [(Z, bind_sub P)]) ++ E).
|
||||||
|
apply sub_weakening...
|
||||||
|
SSCase "Q <: T".
|
||||||
|
binds_get H.
|
||||||
|
inversion H1; subst...
|
||||||
|
SCase "X <> Z".
|
||||||
|
apply (sub_trans_tvar U)...
|
||||||
|
binds_cases H...
|
||||||
|
Case "sub_all".
|
||||||
|
pick fresh Y and apply sub_all...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma sub_transitivity : forall Q,
|
||||||
|
transitivity_on Q.
|
||||||
|
Proof with simpl_env; auto.
|
||||||
|
unfold transitivity_on.
|
||||||
|
intros Q E S T SsubQ QsubT.
|
||||||
|
assert (W : type Q) by auto.
|
||||||
|
generalize dependent T.
|
||||||
|
generalize dependent S.
|
||||||
|
generalize dependent E.
|
||||||
|
remember Q as Q' in |-.
|
||||||
|
generalize dependent Q'.
|
||||||
|
induction W;
|
||||||
|
intros Q' EQ E S SsubQ;
|
||||||
|
induction SsubQ; try discriminate; inversion EQ; subst;
|
||||||
|
intros T' QsubT;
|
||||||
|
inversion QsubT; subst; eauto 4 using sub_trans_tvar.
|
||||||
|
Case "sub_all / sub_top".
|
||||||
|
assert (sub E (typ_all S1 S2) (typ_all T1 T2)).
|
||||||
|
SCase "proof of assertion".
|
||||||
|
pick fresh y and apply sub_all...
|
||||||
|
auto.
|
||||||
|
Case "sub_all / sub_all".
|
||||||
|
pick fresh Y and apply sub_all.
|
||||||
|
SCase "bounds".
|
||||||
|
eauto.
|
||||||
|
SCase "bodies".
|
||||||
|
lapply (H0 Y); [ intros K | auto ].
|
||||||
|
apply (K (open_tt T2 Y))...
|
||||||
|
rewrite_env (empty ++ [(Y, bind_sub T0)] ++ E).
|
||||||
|
apply (sub_narrowing_aux T1)...
|
||||||
|
unfold transitivity_on.
|
||||||
|
auto using (IHW T1).
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma sub_narrowing : forall Q E F Z P S T,
|
||||||
|
sub E P Q ->
|
||||||
|
sub (F ++ [(Z, bind_sub Q)] ++ E) S T ->
|
||||||
|
sub (F ++ [(Z, bind_sub P)] ++ E) S T.
|
||||||
|
Proof.
|
||||||
|
intros.
|
||||||
|
eapply sub_narrowing_aux; eauto.
|
||||||
|
apply sub_transitivity.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Type substitution preserves subtyping (10) *)
|
||||||
|
|
||||||
|
Lemma sub_through_subst_tt : forall Q E F Z S T P,
|
||||||
|
sub (F ++ [(Z, bind_sub Q)] ++ E) S T ->
|
||||||
|
sub E P Q ->
|
||||||
|
sub (map (subst_tb Z P) F ++ E) (subst_tt Z P S) (subst_tt Z P T).
|
||||||
|
Proof with
|
||||||
|
simpl_env;
|
||||||
|
eauto 4 using wf_typ_subst_tb, wf_env_subst_tb, wf_typ_weaken_head.
|
||||||
|
intros Q E F Z S T P SsubT PsubQ.
|
||||||
|
remember (F ++ [(Z, bind_sub Q)] ++ E) as G.
|
||||||
|
generalize dependent F.
|
||||||
|
induction SsubT; intros G EQ; subst; simpl subst_tt...
|
||||||
|
Case "sub_top".
|
||||||
|
apply sub_top...
|
||||||
|
Case "sub_refl_tvar".
|
||||||
|
destruct (X == Z); subst.
|
||||||
|
SCase "X = Z".
|
||||||
|
apply sub_reflexivity...
|
||||||
|
SCase "X <> Z".
|
||||||
|
apply sub_reflexivity...
|
||||||
|
inversion H0; subst.
|
||||||
|
binds_cases H3...
|
||||||
|
apply (wf_typ_var (subst_tt Z P U))...
|
||||||
|
Case "sub_trans_tvar".
|
||||||
|
destruct (X == Z); subst.
|
||||||
|
SCase "X = Z".
|
||||||
|
apply (sub_transitivity Q).
|
||||||
|
SSCase "left branch".
|
||||||
|
rewrite_env (empty ++ map (subst_tb Z P) G ++ E).
|
||||||
|
apply sub_weakening...
|
||||||
|
SSCase "right branch".
|
||||||
|
rewrite (subst_tt_fresh Z P Q).
|
||||||
|
binds_get H.
|
||||||
|
inversion H1; subst...
|
||||||
|
apply (notin_fv_wf E); eauto using fresh_mid_tail.
|
||||||
|
SCase "X <> Z".
|
||||||
|
apply (sub_trans_tvar (subst_tt Z P U))...
|
||||||
|
rewrite (map_subst_tb_id E Z P);
|
||||||
|
[ | auto | eapply fresh_mid_tail; eauto ].
|
||||||
|
binds_cases H...
|
||||||
|
Case "sub_all".
|
||||||
|
pick fresh X and apply sub_all...
|
||||||
|
rewrite subst_tt_open_tt_var...
|
||||||
|
rewrite subst_tt_open_tt_var...
|
||||||
|
rewrite_env (map (subst_tb Z P) ([(X, bind_sub T1)] ++ G) ++ E).
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="typing"></a># Properties of typing *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Weakening (5) *)
|
||||||
|
|
||||||
|
Lemma typing_weakening : forall E F G e T,
|
||||||
|
typing (G ++ E) e T ->
|
||||||
|
wf_env (G ++ F ++ E) ->
|
||||||
|
typing (G ++ F ++ E) e T.
|
||||||
|
Proof with simpl_env;
|
||||||
|
eauto using wf_typ_weakening,
|
||||||
|
wf_typ_from_wf_env_typ,
|
||||||
|
wf_typ_from_wf_env_sub,
|
||||||
|
sub_weakening.
|
||||||
|
intros E F G e T Typ.
|
||||||
|
remember (G ++ E) as H.
|
||||||
|
generalize dependent G.
|
||||||
|
induction Typ; intros G EQ Ok; subst...
|
||||||
|
Case "typing_abs".
|
||||||
|
pick fresh x and apply typing_abs.
|
||||||
|
lapply (H x); [intros K | auto].
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply (H0 x)...
|
||||||
|
Case "typing_tabs".
|
||||||
|
pick fresh X and apply typing_tabs.
|
||||||
|
lapply (H X); [intros K | auto].
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply (H0 X)...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Strengthening (6) *)
|
||||||
|
|
||||||
|
Lemma sub_strengthening : forall x U E F S T,
|
||||||
|
sub (F ++ [(x, bind_typ U)] ++ E) S T ->
|
||||||
|
sub (F ++ E) S T.
|
||||||
|
Proof with eauto using wf_typ_strengthening, wf_env_strengthening.
|
||||||
|
intros x U E F S T SsubT.
|
||||||
|
remember (F ++ [(x, bind_typ U)] ++ E) as E'.
|
||||||
|
generalize dependent F.
|
||||||
|
induction SsubT; intros F EQ; subst...
|
||||||
|
Case "sub_trans_tvar".
|
||||||
|
apply (sub_trans_tvar U0)...
|
||||||
|
binds_cases H...
|
||||||
|
Case "sub_all".
|
||||||
|
pick fresh X and apply sub_all...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(************************************************************************ *)
|
||||||
|
(** ** Narrowing for typing (7) *)
|
||||||
|
|
||||||
|
Lemma typing_narrowing : forall Q E F X P e T,
|
||||||
|
sub E P Q ->
|
||||||
|
typing (F ++ [(X, bind_sub Q)] ++ E) e T ->
|
||||||
|
typing (F ++ [(X, bind_sub P)] ++ E) e T.
|
||||||
|
Proof with eauto 6 using wf_env_narrowing, wf_typ_narrowing, sub_narrowing.
|
||||||
|
intros Q E F X P e T PsubQ Typ.
|
||||||
|
remember (F ++ [(X, bind_sub Q)] ++ E) as E'.
|
||||||
|
generalize dependent F.
|
||||||
|
induction Typ; intros F EQ; subst...
|
||||||
|
Case "typing_var".
|
||||||
|
binds_cases H0...
|
||||||
|
Case "typing_abs".
|
||||||
|
pick fresh y and apply typing_abs.
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Case "typing_tabs".
|
||||||
|
pick fresh Y and apply typing_tabs.
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(************************************************************************ *)
|
||||||
|
(** ** Substitution preserves typing (8) *)
|
||||||
|
|
||||||
|
Lemma typing_through_subst_ee : forall U E F x T e u,
|
||||||
|
typing (F ++ [(x, bind_typ U)] ++ E) e T ->
|
||||||
|
typing E u U ->
|
||||||
|
typing (F ++ E) (subst_ee x u e) T.
|
||||||
|
(* begin show *)
|
||||||
|
|
||||||
|
(** We provide detailed comments for the following proof, mainly to
|
||||||
|
point out several useful tactics and proof techniques.
|
||||||
|
|
||||||
|
Starting a proof with "Proof with <some tactic>" allows us to
|
||||||
|
specify a default tactic that should be used to solve goals. To
|
||||||
|
invoke this default tactic at the end of a proof step, we signal
|
||||||
|
the end of the step with three periods instead of a single one,
|
||||||
|
e.g., "apply typing_weakening...". *)
|
||||||
|
|
||||||
|
Proof with simpl_env;
|
||||||
|
eauto 4 using wf_typ_strengthening,
|
||||||
|
wf_env_strengthening,
|
||||||
|
sub_strengthening.
|
||||||
|
|
||||||
|
(** The proof proceeds by induction on the given typing derivation
|
||||||
|
for e. We use the remember tactic, along with generalize
|
||||||
|
dependent, to ensure that the goal is properly strengthened
|
||||||
|
before we use induction. *)
|
||||||
|
|
||||||
|
intros U E F x T e u TypT TypU.
|
||||||
|
remember (F ++ [(x, bind_typ U)] ++ E) as E'.
|
||||||
|
generalize dependent F.
|
||||||
|
induction TypT; intros F EQ; subst; simpl subst_ee...
|
||||||
|
|
||||||
|
(** The typing_var case involves a case analysis on whether the
|
||||||
|
variable is the same as the one being substituted for. *)
|
||||||
|
|
||||||
|
Case "typing_var".
|
||||||
|
destruct (x0 == x); subst.
|
||||||
|
|
||||||
|
(** In the case where x0=x, we first observe that hypothesis H0
|
||||||
|
implies that T=U, since x can only be bound once in the
|
||||||
|
environment. The conclusion then follows from hypothesis TypU
|
||||||
|
and weakening. We can use the binds_get tactic, described in
|
||||||
|
the Environment library, with H0 to obtain the fact that
|
||||||
|
T=U. *)
|
||||||
|
|
||||||
|
SCase "x0 = x".
|
||||||
|
binds_get H0.
|
||||||
|
inversion H2; subst.
|
||||||
|
|
||||||
|
(** In order to apply typing_weakening, we need to rewrite the
|
||||||
|
environment so that it has the right shape. (We could
|
||||||
|
also prove a corollary of typing_weakening.) The
|
||||||
|
rewrite_env tactic, described in the Environment library,
|
||||||
|
is one way to perform this rewriting. *)
|
||||||
|
|
||||||
|
rewrite_env (empty ++ F ++ E).
|
||||||
|
apply typing_weakening...
|
||||||
|
|
||||||
|
(** In the case where x0<>x, the result follows by an exhaustive
|
||||||
|
case analysis on exactly where x0 is bound in the environment.
|
||||||
|
We perform this case analysis by using the binds_cases tactic,
|
||||||
|
described in the Environment library. *)
|
||||||
|
|
||||||
|
SCase "x0 <> x".
|
||||||
|
binds_cases H0.
|
||||||
|
eauto using wf_env_strengthening.
|
||||||
|
eauto using wf_env_strengthening.
|
||||||
|
|
||||||
|
(** Informally, the typing_abs case is a straightforward application
|
||||||
|
of the induction hypothesis, which is called H0 here. *)
|
||||||
|
|
||||||
|
Case "typing_abs".
|
||||||
|
|
||||||
|
(** We use the "pick fresh and apply" tactic to apply the rule
|
||||||
|
typing_abs without having to calculate the appropriate finite
|
||||||
|
set of atoms. *)
|
||||||
|
|
||||||
|
pick fresh y and apply typing_abs.
|
||||||
|
|
||||||
|
(** We cannot apply H0 directly here. The first problem is that
|
||||||
|
the induction hypothesis has (subst_ee open_ee), whereas in
|
||||||
|
the goal we have (open_ee subst_ee). The lemma
|
||||||
|
subst_ee_open_ee_var lets us swap the order of these two
|
||||||
|
operations. *)
|
||||||
|
|
||||||
|
rewrite subst_ee_open_ee_var...
|
||||||
|
|
||||||
|
(** The second problem is how the concatenations are associated in
|
||||||
|
the environments. In the goal, we currently have
|
||||||
|
|
||||||
|
<< ([(y, bind_typ V)] ++ F ++ E),
|
||||||
|
>>
|
||||||
|
where concatenation associates to the right. In order to
|
||||||
|
apply the induction hypothesis, we need
|
||||||
|
|
||||||
|
<< (([(y, bind_typ V)] ++ F) ++ E).
|
||||||
|
>>
|
||||||
|
We can use the rewrite_env tactic to perform this rewriting,
|
||||||
|
or we can rewrite directly with an appropriate lemma from the
|
||||||
|
Environment library. *)
|
||||||
|
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
|
||||||
|
(** Now we can apply the induction hypothesis. *)
|
||||||
|
|
||||||
|
apply H0...
|
||||||
|
|
||||||
|
(** The remaining cases in this proof are straightforward, given
|
||||||
|
everything that we have pointed out above. *)
|
||||||
|
|
||||||
|
Case "typing_tabs".
|
||||||
|
pick fresh Y and apply typing_tabs.
|
||||||
|
rewrite subst_ee_open_te_var...
|
||||||
|
rewrite <- concat_assoc.
|
||||||
|
apply H0...
|
||||||
|
Qed.
|
||||||
|
(* end show *)
|
||||||
|
|
||||||
|
|
||||||
|
(************************************************************************ *)
|
||||||
|
(** ** Type substitution preserves typing (11) *)
|
||||||
|
|
||||||
|
Lemma typing_through_subst_te : forall Q E F Z e T P,
|
||||||
|
typing (F ++ [(Z, bind_sub Q)] ++ E) e T ->
|
||||||
|
sub E P Q ->
|
||||||
|
typing (map (subst_tb Z P) F ++ E) (subst_te Z P e) (subst_tt Z P T).
|
||||||
|
Proof with simpl_env;
|
||||||
|
eauto 6 using wf_env_subst_tb,
|
||||||
|
wf_typ_subst_tb,
|
||||||
|
sub_through_subst_tt.
|
||||||
|
intros Q E F Z e T P Typ PsubQ.
|
||||||
|
remember (F ++ [(Z, bind_sub Q)] ++ E) as G.
|
||||||
|
generalize dependent F.
|
||||||
|
induction Typ; intros F EQ; subst;
|
||||||
|
simpl subst_te in *; simpl subst_tt in *...
|
||||||
|
Case "typing_var".
|
||||||
|
apply typing_var...
|
||||||
|
rewrite (map_subst_tb_id E Z P);
|
||||||
|
[ | auto | eapply fresh_mid_tail; eauto ].
|
||||||
|
binds_cases H0...
|
||||||
|
Case "typing_abs".
|
||||||
|
pick fresh y and apply typing_abs.
|
||||||
|
rewrite subst_te_open_ee_var...
|
||||||
|
rewrite_env (map (subst_tb Z P) ([(y, bind_typ V)] ++ F) ++ E).
|
||||||
|
apply H0...
|
||||||
|
Case "typing_tabs".
|
||||||
|
pick fresh Y and apply typing_tabs.
|
||||||
|
rewrite subst_te_open_te_var...
|
||||||
|
rewrite subst_tt_open_tt_var...
|
||||||
|
rewrite_env (map (subst_tb Z P) ([(Y, bind_sub V)] ++ F) ++ E).
|
||||||
|
apply H0...
|
||||||
|
Case "typing_tapp".
|
||||||
|
rewrite subst_tt_open_tt...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="preservation"></a># Preservation *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Inversion of typing (13) *)
|
||||||
|
|
||||||
|
Lemma typing_inv_abs : forall E S1 e1 T,
|
||||||
|
typing E (exp_abs S1 e1) T ->
|
||||||
|
forall U1 U2, sub E T (typ_arrow U1 U2) ->
|
||||||
|
sub E U1 S1
|
||||||
|
/\ exists S2, exists L, forall x, x `notin` L ->
|
||||||
|
typing ([(x, bind_typ S1)] ++ E) (open_ee e1 x) S2 /\ sub E S2 U2.
|
||||||
|
Proof with auto.
|
||||||
|
intros E S1 e1 T Typ.
|
||||||
|
remember (exp_abs S1 e1) as e.
|
||||||
|
generalize dependent e1.
|
||||||
|
generalize dependent S1.
|
||||||
|
induction Typ; intros S1 b1 EQ U1 U2 Sub; inversion EQ; subst.
|
||||||
|
Case "typing_abs".
|
||||||
|
inversion Sub; subst.
|
||||||
|
split...
|
||||||
|
exists T1. exists L...
|
||||||
|
Case "typing_sub".
|
||||||
|
auto using (sub_transitivity T).
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma typing_inv_tabs : forall E S1 e1 T,
|
||||||
|
typing E (exp_tabs S1 e1) T ->
|
||||||
|
forall U1 U2, sub E T (typ_all U1 U2) ->
|
||||||
|
sub E U1 S1
|
||||||
|
/\ exists S2, exists L, forall X, X `notin` L ->
|
||||||
|
typing ([(X, bind_sub U1)] ++ E) (open_te e1 X) (open_tt S2 X)
|
||||||
|
/\ sub ([(X, bind_sub U1)] ++ E) (open_tt S2 X) (open_tt U2 X).
|
||||||
|
Proof with simpl_env; auto.
|
||||||
|
intros E S1 e1 T Typ.
|
||||||
|
remember (exp_tabs S1 e1) as e.
|
||||||
|
generalize dependent e1.
|
||||||
|
generalize dependent S1.
|
||||||
|
induction Typ; intros S1 e0 EQ U1 U2 Sub; inversion EQ; subst.
|
||||||
|
Case "typing_tabs".
|
||||||
|
inversion Sub; subst.
|
||||||
|
split...
|
||||||
|
exists T1.
|
||||||
|
exists (L0 `union` L).
|
||||||
|
intros Y Fr.
|
||||||
|
split...
|
||||||
|
rewrite_env (empty ++ [(Y, bind_sub U1)] ++ E).
|
||||||
|
apply (typing_narrowing S1)...
|
||||||
|
Case "typing_sub".
|
||||||
|
auto using (sub_transitivity T).
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Preservation (20) *)
|
||||||
|
|
||||||
|
Lemma preservation : forall E e e' T,
|
||||||
|
typing E e T ->
|
||||||
|
red e e' ->
|
||||||
|
typing E e' T.
|
||||||
|
Proof with simpl_env; eauto.
|
||||||
|
intros E e e' T Typ. generalize dependent e'.
|
||||||
|
induction Typ; intros e' Red; try solve [ inversion Red; subst; eauto ].
|
||||||
|
Case "typing_app".
|
||||||
|
inversion Red; subst...
|
||||||
|
SCase "red_abs".
|
||||||
|
destruct (typing_inv_abs _ _ _ _ Typ1 T1 T2) as [P1 [S2 [L P2]]].
|
||||||
|
apply sub_reflexivity...
|
||||||
|
pick fresh x.
|
||||||
|
destruct (P2 x) as [? ?]...
|
||||||
|
rewrite (subst_ee_intro x)...
|
||||||
|
rewrite_env (empty ++ E).
|
||||||
|
apply (typing_through_subst_ee T).
|
||||||
|
apply (typing_sub S2)...
|
||||||
|
rewrite_env (empty ++ [(x, bind_typ T)] ++ E).
|
||||||
|
apply sub_weakening...
|
||||||
|
eauto.
|
||||||
|
Case "typing_tapp".
|
||||||
|
inversion Red; subst...
|
||||||
|
SCase "red_tabs".
|
||||||
|
destruct (typing_inv_tabs _ _ _ _ Typ T1 T2) as [P1 [S2 [L P2]]].
|
||||||
|
apply sub_reflexivity...
|
||||||
|
pick fresh X.
|
||||||
|
destruct (P2 X) as [? ?]...
|
||||||
|
rewrite (subst_te_intro X)...
|
||||||
|
rewrite (subst_tt_intro X)...
|
||||||
|
rewrite_env (map (subst_tb X T) empty ++ E).
|
||||||
|
apply (typing_through_subst_te T1)...
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** * #<a name="progress"></a># Progress *)
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Canonical forms (14) *)
|
||||||
|
|
||||||
|
Lemma canonical_form_abs : forall e U1 U2,
|
||||||
|
value e ->
|
||||||
|
typing empty e (typ_arrow U1 U2) ->
|
||||||
|
exists V, exists e1, e = exp_abs V e1.
|
||||||
|
Proof.
|
||||||
|
intros e U1 U2 Val Typ.
|
||||||
|
remember empty as E.
|
||||||
|
remember (typ_arrow U1 U2) as T.
|
||||||
|
revert U1 U2 HeqT HeqE.
|
||||||
|
induction Typ; intros U1 U2 EQT EQE; subst;
|
||||||
|
try solve [ inversion Val | inversion EQT | eauto ].
|
||||||
|
Case "typing_sub".
|
||||||
|
inversion H; subst; eauto.
|
||||||
|
inversion H0.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
Lemma canonical_form_tabs : forall e U1 U2,
|
||||||
|
value e ->
|
||||||
|
typing empty e (typ_all U1 U2) ->
|
||||||
|
exists V, exists e1, e = exp_tabs V e1.
|
||||||
|
Proof.
|
||||||
|
intros e U1 U2 Val Typ.
|
||||||
|
remember empty as E.
|
||||||
|
remember (typ_all U1 U2) as T.
|
||||||
|
revert U1 U2 HeqT HeqT.
|
||||||
|
induction Typ; intros U1 U2 EQT EQE; subst;
|
||||||
|
try solve [ inversion Val | inversion EQT | eauto ].
|
||||||
|
Case "typing_sub".
|
||||||
|
inversion H; subst; eauto.
|
||||||
|
inversion H0.
|
||||||
|
Qed.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
(* ********************************************************************** *)
|
||||||
|
(** ** Progress (16) *)
|
||||||
|
|
||||||
|
Lemma progress : forall e T,
|
||||||
|
typing empty e T ->
|
||||||
|
value e \/ exists e', red e e'.
|
||||||
|
Proof with eauto.
|
||||||
|
intros e T Typ.
|
||||||
|
remember empty as E. generalize dependent HeqE.
|
||||||
|
assert (Typ' : typing E e T)...
|
||||||
|
induction Typ; intros EQ; subst...
|
||||||
|
Case "typing_var".
|
||||||
|
inversion H0.
|
||||||
|
Case "typing_app".
|
||||||
|
right.
|
||||||
|
destruct IHTyp1 as [Val1 | [e1' Rede1']]...
|
||||||
|
SCase "Val1".
|
||||||
|
destruct IHTyp2 as [Val2 | [e2' Rede2']]...
|
||||||
|
SSCase "Val2".
|
||||||
|
destruct (canonical_form_abs _ _ _ Val1 Typ1) as [S [e3 EQ]].
|
||||||
|
subst.
|
||||||
|
exists (open_ee e3 e2)...
|
||||||
|
Case "typing_tapp".
|
||||||
|
right.
|
||||||
|
destruct IHTyp as [Val1 | [e1' Rede1']]...
|
||||||
|
SCase "Val1".
|
||||||
|
destruct (canonical_form_tabs _ _ _ Val1 Typ) as [S [e3 EQ]].
|
||||||
|
subst.
|
||||||
|
exists (open_te e3 T)...
|
||||||
|
SCase "e1' Rede1'".
|
||||||
|
exists (exp_tapp e1' T)...
|
||||||
|
Qed.
|
||||||
999
share/popl08-tutorial-Fsub/Makefile
Normal file
|
|
@ -0,0 +1,999 @@
|
||||||
|
##########################################################################
|
||||||
|
## # The Coq Proof Assistant / The Coq Development Team ##
|
||||||
|
## v # Copyright INRIA, CNRS and contributors ##
|
||||||
|
## <O___,, # (see version control and CREDITS file for authors & dates) ##
|
||||||
|
## \VV/ ###############################################################
|
||||||
|
## // # This file is distributed under the terms of the ##
|
||||||
|
## # GNU Lesser General Public License Version 2.1 ##
|
||||||
|
## # (see LICENSE file for the text of the license) ##
|
||||||
|
##########################################################################
|
||||||
|
## GNUMakefile for Coq 8.19.2
|
||||||
|
|
||||||
|
# For debugging purposes (must stay here, don't move below)
|
||||||
|
INITIAL_VARS := $(.VARIABLES)
|
||||||
|
# To implement recursion we save the name of the main Makefile
|
||||||
|
SELF := $(lastword $(MAKEFILE_LIST))
|
||||||
|
PARENT := $(firstword $(MAKEFILE_LIST))
|
||||||
|
|
||||||
|
# This file is generated by coq_makefile and contains many variable
|
||||||
|
# definitions, like the list of .v files or the path to Coq
|
||||||
|
include Makefile.conf
|
||||||
|
|
||||||
|
# Put in place old names
|
||||||
|
VFILES := $(COQMF_VFILES)
|
||||||
|
MLIFILES := $(COQMF_MLIFILES)
|
||||||
|
MLFILES := $(COQMF_MLFILES)
|
||||||
|
MLGFILES := $(COQMF_MLGFILES)
|
||||||
|
MLPACKFILES := $(COQMF_MLPACKFILES)
|
||||||
|
MLLIBFILES := $(COQMF_MLLIBFILES)
|
||||||
|
METAFILE := $(COQMF_METAFILE)
|
||||||
|
CMDLINE_VFILES := $(COQMF_CMDLINE_VFILES)
|
||||||
|
INSTALLCOQDOCROOT := $(COQMF_INSTALLCOQDOCROOT)
|
||||||
|
OTHERFLAGS := $(COQMF_OTHERFLAGS)
|
||||||
|
COQCORE_SRC_SUBDIRS := $(COQMF_COQ_SRC_SUBDIRS)
|
||||||
|
OCAMLLIBS := $(COQMF_OCAMLLIBS)
|
||||||
|
SRC_SUBDIRS := $(COQMF_SRC_SUBDIRS)
|
||||||
|
COQLIBS := $(COQMF_COQLIBS)
|
||||||
|
COQLIBS_NOML := $(COQMF_COQLIBS_NOML)
|
||||||
|
CMDLINE_COQLIBS := $(COQMF_CMDLINE_COQLIBS)
|
||||||
|
COQLIB := $(COQMF_COQLIB)
|
||||||
|
COQCORELIB := $(COQMF_COQCORELIB)
|
||||||
|
DOCDIR := $(COQMF_DOCDIR)
|
||||||
|
OCAMLFIND := $(COQMF_OCAMLFIND)
|
||||||
|
CAMLFLAGS := $(COQMF_CAMLFLAGS)
|
||||||
|
HASNATDYNLINK := $(COQMF_HASNATDYNLINK)
|
||||||
|
OCAMLWARN := $(COQMF_WARN)
|
||||||
|
|
||||||
|
Makefile.conf: _CoqProject
|
||||||
|
coq_makefile -f _CoqProject -o Makefile
|
||||||
|
|
||||||
|
# This file can be created by the user to hook into double colon rules or
|
||||||
|
# add any other Makefile code he may need
|
||||||
|
-include Makefile.local
|
||||||
|
|
||||||
|
# Parameters ##################################################################
|
||||||
|
#
|
||||||
|
# Parameters are make variable assignments.
|
||||||
|
# They can be passed to (each call to) make on the command line.
|
||||||
|
# They can also be put in Makefile.local once and for all.
|
||||||
|
# For retro-compatibility reasons they can be put in the _CoqProject, but this
|
||||||
|
# practice is discouraged since _CoqProject better not contain make specific
|
||||||
|
# code (be nice to user interfaces).
|
||||||
|
|
||||||
|
# Set KEEP_ERROR to have make keep files produced by failing rules.
|
||||||
|
# By default, KEEP_ERROR is empty. So for instance if coqc creates a .vo but
|
||||||
|
# then fails to native compile, the .vo will be deleted.
|
||||||
|
# May confuse make so use only for debugging.
|
||||||
|
KEEP_ERROR?=
|
||||||
|
ifeq (,$(KEEP_ERROR))
|
||||||
|
.DELETE_ON_ERROR:
|
||||||
|
endif
|
||||||
|
|
||||||
|
# Print shell commands (set to non empty)
|
||||||
|
VERBOSE ?=
|
||||||
|
|
||||||
|
# Time the Coq process (set to non empty), and how (see default value)
|
||||||
|
TIMED?=
|
||||||
|
TIMECMD?=
|
||||||
|
# Use command time on linux, gtime on Mac OS
|
||||||
|
TIMEFMT?="$(if $(findstring undefined, $(flavor 1)),$@,$(1)) (real: %e, user: %U, sys: %S, mem: %M ko)"
|
||||||
|
ifneq (,$(TIMED))
|
||||||
|
ifeq (0,$(shell command time -f "" true >/dev/null 2>/dev/null; echo $$?))
|
||||||
|
STDTIME?=command time -f $(TIMEFMT)
|
||||||
|
else
|
||||||
|
ifeq (0,$(shell gtime -f "" true >/dev/null 2>/dev/null; echo $$?))
|
||||||
|
STDTIME?=gtime -f $(TIMEFMT)
|
||||||
|
else
|
||||||
|
STDTIME?=command time
|
||||||
|
endif
|
||||||
|
endif
|
||||||
|
else
|
||||||
|
STDTIME?=command time -f $(TIMEFMT)
|
||||||
|
endif
|
||||||
|
|
||||||
|
COQBIN?=
|
||||||
|
ifneq (,$(COQBIN))
|
||||||
|
# add an ending /
|
||||||
|
COQBIN:=$(COQBIN)/
|
||||||
|
endif
|
||||||
|
|
||||||
|
# Coq binaries
|
||||||
|
COQC ?= "$(COQBIN)coqc"
|
||||||
|
COQTOP ?= "$(COQBIN)coqtop"
|
||||||
|
COQCHK ?= "$(COQBIN)coqchk"
|
||||||
|
COQNATIVE ?= "$(COQBIN)coqnative"
|
||||||
|
COQDEP ?= "$(COQBIN)coqdep"
|
||||||
|
COQDOC ?= "$(COQBIN)coqdoc"
|
||||||
|
COQPP ?= "$(COQBIN)coqpp"
|
||||||
|
COQMKFILE ?= "$(COQBIN)coq_makefile"
|
||||||
|
OCAMLLIBDEP ?= "$(COQBIN)ocamllibdep"
|
||||||
|
|
||||||
|
# Timing scripts
|
||||||
|
COQMAKE_ONE_TIME_FILE ?= "$(COQCORELIB)/tools/make-one-time-file.py"
|
||||||
|
COQMAKE_BOTH_TIME_FILES ?= "$(COQCORELIB)/tools/make-both-time-files.py"
|
||||||
|
COQMAKE_BOTH_SINGLE_TIMING_FILES ?= "$(COQCORELIB)/tools/make-both-single-timing-files.py"
|
||||||
|
BEFORE ?=
|
||||||
|
AFTER ?=
|
||||||
|
|
||||||
|
# OCaml binaries
|
||||||
|
CAMLC ?= "$(OCAMLFIND)" ocamlc -c
|
||||||
|
CAMLOPTC ?= "$(OCAMLFIND)" opt -c
|
||||||
|
CAMLLINK ?= "$(OCAMLFIND)" ocamlc -linkall
|
||||||
|
CAMLOPTLINK ?= "$(OCAMLFIND)" opt -linkall
|
||||||
|
CAMLDOC ?= "$(OCAMLFIND)" ocamldoc
|
||||||
|
CAMLDEP ?= "$(OCAMLFIND)" ocamldep -slash -ml-synonym .mlpack
|
||||||
|
|
||||||
|
# DESTDIR is prepended to all installation paths
|
||||||
|
DESTDIR ?=
|
||||||
|
|
||||||
|
# Debug builds, typically -g to OCaml, -debug to Coq.
|
||||||
|
CAMLDEBUG ?=
|
||||||
|
COQDEBUG ?=
|
||||||
|
|
||||||
|
# Extra packages to be linked in (as in findlib -package)
|
||||||
|
CAMLPKGS ?=
|
||||||
|
FINDLIBPKGS = -package coq-core.plugins.ltac $(CAMLPKGS)
|
||||||
|
|
||||||
|
# Option for making timing files
|
||||||
|
TIMING?=
|
||||||
|
# Option for changing sorting of timing output file
|
||||||
|
TIMING_SORT_BY ?= auto
|
||||||
|
# Option for changing the fuzz parameter on the output file
|
||||||
|
TIMING_FUZZ ?= 0
|
||||||
|
# Option for changing whether to use real or user time for timing tables
|
||||||
|
TIMING_REAL?=
|
||||||
|
# Option for including the memory column(s)
|
||||||
|
TIMING_INCLUDE_MEM?=
|
||||||
|
# Option for sorting by the memory column
|
||||||
|
TIMING_SORT_BY_MEM?=
|
||||||
|
# Output file names for timed builds
|
||||||
|
TIME_OF_BUILD_FILE ?= time-of-build.log
|
||||||
|
TIME_OF_BUILD_BEFORE_FILE ?= time-of-build-before.log
|
||||||
|
TIME_OF_BUILD_AFTER_FILE ?= time-of-build-after.log
|
||||||
|
TIME_OF_PRETTY_BUILD_FILE ?= time-of-build-pretty.log
|
||||||
|
TIME_OF_PRETTY_BOTH_BUILD_FILE ?= time-of-build-both.log
|
||||||
|
TIME_OF_PRETTY_BUILD_EXTRA_FILES ?= - # also output to the command line
|
||||||
|
|
||||||
|
TGTS ?=
|
||||||
|
|
||||||
|
# Retro compatibility (DESTDIR is standard on Unix, DSTROOT is not)
|
||||||
|
ifdef DSTROOT
|
||||||
|
DESTDIR := $(DSTROOT)
|
||||||
|
endif
|
||||||
|
|
||||||
|
# Substitution of the path by appending $(DESTDIR) if needed.
|
||||||
|
# The variable $(COQMF_WINDRIVE) can be needed for Cygwin environments.
|
||||||
|
windrive_path = $(if $(COQMF_WINDRIVE),$(subst $(COQMF_WINDRIVE),/,$(1)),$(1))
|
||||||
|
destination_path = $(if $(DESTDIR),$(DESTDIR)/$(call windrive_path,$(1)),$(1))
|
||||||
|
|
||||||
|
# Installation paths of libraries and documentation.
|
||||||
|
COQLIBINSTALL ?= $(call destination_path,$(COQLIB)/user-contrib)
|
||||||
|
COQDOCINSTALL ?= $(call destination_path,$(DOCDIR)/coq/user-contrib)
|
||||||
|
COQPLUGININSTALL ?= $(call destination_path,$(COQCORELIB)/..)
|
||||||
|
COQTOPINSTALL ?= $(call destination_path,$(COQLIB)/toploop) # FIXME: Unused variable?
|
||||||
|
|
||||||
|
# findlib files installation
|
||||||
|
FINDLIBPREINST= mkdir -p "$(COQPLUGININSTALL)/"
|
||||||
|
FINDLIBDESTDIR= -destdir "$(COQPLUGININSTALL)/"
|
||||||
|
|
||||||
|
# we need to move out of sight $(METAFILE) otherwise findlib thinks the
|
||||||
|
# package is already installed
|
||||||
|
findlib_install = \
|
||||||
|
$(HIDE)if [ "$(METAFILE)" ]; then \
|
||||||
|
$(FINDLIBPREINST) && \
|
||||||
|
mv "$(METAFILE)" "$(METAFILE).skip" ; \
|
||||||
|
"$(OCAMLFIND)" install $(2) $(FINDLIBDESTDIR) $(FINDLIBPACKAGE) $(1); \
|
||||||
|
rc=$$?; \
|
||||||
|
mv "$(METAFILE).skip" "$(METAFILE)"; \
|
||||||
|
exit $$rc; \
|
||||||
|
fi
|
||||||
|
findlib_remove = \
|
||||||
|
$(HIDE)if [ ! -z "$(METAFILE)" ]; then\
|
||||||
|
"$(OCAMLFIND)" remove $(FINDLIBDESTDIR) $(FINDLIBPACKAGE); \
|
||||||
|
fi
|
||||||
|
|
||||||
|
|
||||||
|
########## End of parameters ##################################################
|
||||||
|
# What follows may be relevant to you only if you need to
|
||||||
|
# extend this Makefile. If so, look for 'Extension point' here and
|
||||||
|
# put in Makefile.local double colon rules accordingly.
|
||||||
|
# E.g. to perform some work after the all target completes you can write
|
||||||
|
#
|
||||||
|
# post-all::
|
||||||
|
# echo "All done!"
|
||||||
|
#
|
||||||
|
# in Makefile.local
|
||||||
|
#
|
||||||
|
###############################################################################
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
# Flags #######################################################################
|
||||||
|
#
|
||||||
|
# We define a bunch of variables combining the parameters.
|
||||||
|
# To add additional flags to coq, coqchk or coqdoc, set the
|
||||||
|
# {COQ,COQCHK,COQDOC}EXTRAFLAGS variable to whatever you want to add.
|
||||||
|
# To overwrite the default choice and set your own flags entirely, set the
|
||||||
|
# {COQ,COQCHK,COQDOC}FLAGS variable.
|
||||||
|
|
||||||
|
SHOW := $(if $(VERBOSE),@true "",@echo "")
|
||||||
|
HIDE := $(if $(VERBOSE),,@)
|
||||||
|
|
||||||
|
TIMER=$(if $(TIMED), $(STDTIME), $(TIMECMD))
|
||||||
|
|
||||||
|
OPT?=
|
||||||
|
|
||||||
|
# The DYNOBJ and DYNLIB variables are used by "coqdep -dyndep var" in .v.d
|
||||||
|
ifeq '$(OPT)' '-byte'
|
||||||
|
USEBYTE:=true
|
||||||
|
DYNOBJ:=.cma
|
||||||
|
DYNLIB:=.cma
|
||||||
|
else
|
||||||
|
USEBYTE:=
|
||||||
|
DYNOBJ:=.cmxs
|
||||||
|
DYNLIB:=.cmxs
|
||||||
|
endif
|
||||||
|
|
||||||
|
# these variables are meant to be overridden if you want to add *extra* flags
|
||||||
|
COQEXTRAFLAGS?=
|
||||||
|
COQCHKEXTRAFLAGS?=
|
||||||
|
COQDOCEXTRAFLAGS?=
|
||||||
|
|
||||||
|
# Find the last argument of the form "-native-compiler FLAG"
|
||||||
|
COQUSERNATIVEFLAG:=$(strip \
|
||||||
|
$(subst -native-compiler-,,\
|
||||||
|
$(lastword \
|
||||||
|
$(filter -native-compiler-%,\
|
||||||
|
$(subst -native-compiler ,-native-compiler-,\
|
||||||
|
$(strip $(COQEXTRAFLAGS)))))))
|
||||||
|
|
||||||
|
COQFILTEREDEXTRAFLAGS:=$(strip \
|
||||||
|
$(filter-out -native-compiler-%,\
|
||||||
|
$(subst -native-compiler ,-native-compiler-,\
|
||||||
|
$(strip $(COQEXTRAFLAGS)))))
|
||||||
|
|
||||||
|
COQACTUALNATIVEFLAG:=$(lastword $(COQMF_COQ_NATIVE_COMPILER_DEFAULT) $(COQMF_COQPROJECTNATIVEFLAG) $(COQUSERNATIVEFLAG))
|
||||||
|
|
||||||
|
ifeq '$(COQACTUALNATIVEFLAG)' 'yes'
|
||||||
|
COQNATIVEFLAG="-w" "-deprecated-native-compiler-option" "-native-compiler" "ondemand"
|
||||||
|
COQDONATIVE="yes"
|
||||||
|
else
|
||||||
|
ifeq '$(COQACTUALNATIVEFLAG)' 'ondemand'
|
||||||
|
COQNATIVEFLAG="-w" "-deprecated-native-compiler-option" "-native-compiler" "ondemand"
|
||||||
|
COQDONATIVE="no"
|
||||||
|
else
|
||||||
|
COQNATIVEFLAG="-w" "-deprecated-native-compiler-option" "-native-compiler" "no"
|
||||||
|
COQDONATIVE="no"
|
||||||
|
endif
|
||||||
|
endif
|
||||||
|
|
||||||
|
# these flags do NOT contain the libraries, to make them easier to overwrite
|
||||||
|
COQFLAGS?=-q $(OTHERFLAGS) $(COQFILTEREDEXTRAFLAGS) $(COQNATIVEFLAG)
|
||||||
|
COQCHKFLAGS?=-silent -o $(COQCHKEXTRAFLAGS)
|
||||||
|
COQDOCFLAGS?=-interpolate -utf8 $(COQDOCEXTRAFLAGS)
|
||||||
|
|
||||||
|
COQDOCLIBS?=$(COQLIBS_NOML)
|
||||||
|
|
||||||
|
# The version of Coq being run and the version of coq_makefile that
|
||||||
|
# generated this makefile
|
||||||
|
COQ_VERSION:=$(shell $(COQC) --print-version | cut -d " " -f 1)
|
||||||
|
COQMAKEFILE_VERSION:=8.19.2
|
||||||
|
|
||||||
|
# COQ_SRC_SUBDIRS is for user-overriding, usually to add
|
||||||
|
# `user-contrib/Foo` to the includes, we keep COQCORE_SRC_SUBDIRS for
|
||||||
|
# Coq's own core libraries, which should be replaced by ocamlfind
|
||||||
|
# options at some point.
|
||||||
|
COQ_SRC_SUBDIRS?=
|
||||||
|
COQSRCLIBS?= $(foreach d,$(COQ_SRC_SUBDIRS), -I "$(COQLIB)/$(d)")
|
||||||
|
|
||||||
|
CAMLFLAGS+=$(OCAMLLIBS) $(COQSRCLIBS)
|
||||||
|
# ocamldoc fails with unknown argument otherwise
|
||||||
|
CAMLDOCFLAGS:=$(filter-out -annot, $(filter-out -bin-annot, $(CAMLFLAGS)))
|
||||||
|
CAMLFLAGS+=$(OCAMLWARN)
|
||||||
|
|
||||||
|
ifneq (,$(TIMING))
|
||||||
|
ifeq (after,$(TIMING))
|
||||||
|
TIMING_EXT=after-timing
|
||||||
|
else
|
||||||
|
ifeq (before,$(TIMING))
|
||||||
|
TIMING_EXT=before-timing
|
||||||
|
else
|
||||||
|
TIMING_EXT=timing
|
||||||
|
endif
|
||||||
|
endif
|
||||||
|
TIMING_ARG=-time-file $<.$(TIMING_EXT)
|
||||||
|
else
|
||||||
|
TIMING_ARG=
|
||||||
|
endif
|
||||||
|
|
||||||
|
ifneq (,$(PROFILING))
|
||||||
|
PROFILE_ARG=-profile $<.prof.json
|
||||||
|
PROFILE_ZIP=gzip $<.prof.json
|
||||||
|
else
|
||||||
|
PROFILE_ARG=
|
||||||
|
PROFILE_ZIP=true
|
||||||
|
endif
|
||||||
|
|
||||||
|
# Files #######################################################################
|
||||||
|
#
|
||||||
|
# We here define a bunch of variables about the files being part of the
|
||||||
|
# Coq project in order to ease the writing of build target and build rules
|
||||||
|
|
||||||
|
VDFILE := .Makefile.d
|
||||||
|
|
||||||
|
ALLSRCFILES := \
|
||||||
|
$(MLGFILES) \
|
||||||
|
$(MLFILES) \
|
||||||
|
$(MLPACKFILES) \
|
||||||
|
$(MLLIBFILES) \
|
||||||
|
$(MLIFILES)
|
||||||
|
|
||||||
|
# helpers
|
||||||
|
vo_to_obj = $(addsuffix .o,\
|
||||||
|
$(filter-out Warning: Error:,\
|
||||||
|
$(shell $(COQTOP) -q -noinit -batch -quiet -print-mod-uid $(1))))
|
||||||
|
strip_dotslash = $(patsubst ./%,%,$(1))
|
||||||
|
|
||||||
|
# without this we get undefined variables in the expansion for the
|
||||||
|
# targets of the [deprecated,use-mllib-or-mlpack] rule
|
||||||
|
with_undef = $(if $(filter-out undefined, $(origin $(1))),$($(1)))
|
||||||
|
|
||||||
|
VO = vo
|
||||||
|
VOS = vos
|
||||||
|
|
||||||
|
VOFILES = $(VFILES:.v=.$(VO))
|
||||||
|
GLOBFILES = $(VFILES:.v=.glob)
|
||||||
|
HTMLFILES = $(VFILES:.v=.html)
|
||||||
|
GHTMLFILES = $(VFILES:.v=.g.html)
|
||||||
|
BEAUTYFILES = $(addsuffix .beautified,$(VFILES))
|
||||||
|
TEXFILES = $(VFILES:.v=.tex)
|
||||||
|
GTEXFILES = $(VFILES:.v=.g.tex)
|
||||||
|
CMOFILES = \
|
||||||
|
$(MLGFILES:.mlg=.cmo) \
|
||||||
|
$(MLFILES:.ml=.cmo) \
|
||||||
|
$(MLPACKFILES:.mlpack=.cmo)
|
||||||
|
CMXFILES = $(CMOFILES:.cmo=.cmx)
|
||||||
|
OFILES = $(CMXFILES:.cmx=.o)
|
||||||
|
CMAFILES = $(MLLIBFILES:.mllib=.cma) $(MLPACKFILES:.mlpack=.cma)
|
||||||
|
CMXAFILES = $(CMAFILES:.cma=.cmxa)
|
||||||
|
CMIFILES = \
|
||||||
|
$(CMOFILES:.cmo=.cmi) \
|
||||||
|
$(MLIFILES:.mli=.cmi)
|
||||||
|
# the /if/ is because old _CoqProject did not list a .ml(pack|lib) but just
|
||||||
|
# a .mlg file
|
||||||
|
CMXSFILES = \
|
||||||
|
$(MLPACKFILES:.mlpack=.cmxs) \
|
||||||
|
$(CMXAFILES:.cmxa=.cmxs) \
|
||||||
|
$(if $(MLPACKFILES)$(CMXAFILES),,\
|
||||||
|
$(MLGFILES:.mlg=.cmxs) $(MLFILES:.ml=.cmxs))
|
||||||
|
|
||||||
|
# files that are packed into a plugin (no extension)
|
||||||
|
PACKEDFILES = \
|
||||||
|
$(call strip_dotslash, \
|
||||||
|
$(foreach lib, \
|
||||||
|
$(call strip_dotslash, \
|
||||||
|
$(MLPACKFILES:.mlpack=_MLPACK_DEPENDENCIES)),$(call with_undef,$(lib))))
|
||||||
|
# files that are archived into a .cma (mllib)
|
||||||
|
LIBEDFILES = \
|
||||||
|
$(call strip_dotslash, \
|
||||||
|
$(foreach lib, \
|
||||||
|
$(call strip_dotslash, \
|
||||||
|
$(MLLIBFILES:.mllib=_MLLIB_DEPENDENCIES)),$(call with_undef,$(lib))))
|
||||||
|
CMIFILESTOINSTALL = $(filter-out $(addsuffix .cmi,$(PACKEDFILES)),$(CMIFILES))
|
||||||
|
CMOFILESTOINSTALL = $(filter-out $(addsuffix .cmo,$(PACKEDFILES)),$(CMOFILES))
|
||||||
|
OBJFILES = $(call vo_to_obj,$(VOFILES))
|
||||||
|
ALLNATIVEFILES = \
|
||||||
|
$(OBJFILES:.o=.cmi) \
|
||||||
|
$(OBJFILES:.o=.cmx) \
|
||||||
|
$(OBJFILES:.o=.cmxs)
|
||||||
|
FINDLIBPACKAGE=$(patsubst .%,%,$(suffix $(METAFILE)))
|
||||||
|
|
||||||
|
# trick: wildcard filters out non-existing files, so that `install` doesn't show
|
||||||
|
# warnings and `clean` doesn't pass to rm a list of files that is too long for
|
||||||
|
# the shell.
|
||||||
|
NATIVEFILES = $(wildcard $(ALLNATIVEFILES))
|
||||||
|
FILESTOINSTALL = \
|
||||||
|
$(VOFILES) \
|
||||||
|
$(VFILES) \
|
||||||
|
$(GLOBFILES) \
|
||||||
|
$(NATIVEFILES) \
|
||||||
|
$(CMXSFILES) # to be removed when we remove legacy loading
|
||||||
|
FINDLIBFILESTOINSTALL = \
|
||||||
|
$(CMIFILESTOINSTALL)
|
||||||
|
ifeq '$(HASNATDYNLINK)' 'true'
|
||||||
|
DO_NATDYNLINK = yes
|
||||||
|
FINDLIBFILESTOINSTALL += $(CMXSFILES) $(CMXAFILES) $(CMOFILESTOINSTALL:.cmo=.cmx)
|
||||||
|
else
|
||||||
|
DO_NATDYNLINK =
|
||||||
|
endif
|
||||||
|
|
||||||
|
ALLDFILES = $(addsuffix .d,$(ALLSRCFILES)) $(VDFILE)
|
||||||
|
|
||||||
|
# Compilation targets #########################################################
|
||||||
|
|
||||||
|
all:
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" pre-all
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" real-all
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" post-all
|
||||||
|
.PHONY: all
|
||||||
|
|
||||||
|
all.timing.diff:
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" pre-all
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" real-all.timing.diff TIME_OF_PRETTY_BUILD_EXTRA_FILES=""
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" post-all
|
||||||
|
.PHONY: all.timing.diff
|
||||||
|
|
||||||
|
ifeq (0,$(TIMING_REAL))
|
||||||
|
TIMING_REAL_ARG :=
|
||||||
|
TIMING_USER_ARG := --user
|
||||||
|
else
|
||||||
|
ifeq (1,$(TIMING_REAL))
|
||||||
|
TIMING_REAL_ARG := --real
|
||||||
|
TIMING_USER_ARG :=
|
||||||
|
else
|
||||||
|
TIMING_REAL_ARG :=
|
||||||
|
TIMING_USER_ARG :=
|
||||||
|
endif
|
||||||
|
endif
|
||||||
|
|
||||||
|
ifeq (0,$(TIMING_INCLUDE_MEM))
|
||||||
|
TIMING_INCLUDE_MEM_ARG := --no-include-mem
|
||||||
|
else
|
||||||
|
TIMING_INCLUDE_MEM_ARG :=
|
||||||
|
endif
|
||||||
|
|
||||||
|
ifeq (1,$(TIMING_SORT_BY_MEM))
|
||||||
|
TIMING_SORT_BY_MEM_ARG := --sort-by-mem
|
||||||
|
else
|
||||||
|
TIMING_SORT_BY_MEM_ARG :=
|
||||||
|
endif
|
||||||
|
|
||||||
|
make-pretty-timed-before:: TIME_OF_BUILD_FILE=$(TIME_OF_BUILD_BEFORE_FILE)
|
||||||
|
make-pretty-timed-after:: TIME_OF_BUILD_FILE=$(TIME_OF_BUILD_AFTER_FILE)
|
||||||
|
make-pretty-timed make-pretty-timed-before make-pretty-timed-after::
|
||||||
|
$(HIDE)rm -f pretty-timed-success.ok
|
||||||
|
$(HIDE)($(MAKE) --no-print-directory -f "$(PARENT)" $(TGTS) TIMED=1 2>&1 && touch pretty-timed-success.ok) | tee -a $(TIME_OF_BUILD_FILE)
|
||||||
|
$(HIDE)rm pretty-timed-success.ok # must not be -f; must fail if the touch failed
|
||||||
|
print-pretty-timed::
|
||||||
|
$(HIDE)$(COQMAKE_ONE_TIME_FILE) $(TIMING_INCLUDE_MEM_ARG) $(TIMING_SORT_BY_MEM_ARG) $(TIMING_REAL_ARG) $(TIME_OF_BUILD_FILE) $(TIME_OF_PRETTY_BUILD_FILE) $(TIME_OF_PRETTY_BUILD_EXTRA_FILES)
|
||||||
|
print-pretty-timed-diff::
|
||||||
|
$(HIDE)$(COQMAKE_BOTH_TIME_FILES) --sort-by=$(TIMING_SORT_BY) $(TIMING_INCLUDE_MEM_ARG) $(TIMING_SORT_BY_MEM_ARG) $(TIMING_REAL_ARG) $(TIME_OF_BUILD_AFTER_FILE) $(TIME_OF_BUILD_BEFORE_FILE) $(TIME_OF_PRETTY_BOTH_BUILD_FILE) $(TIME_OF_PRETTY_BUILD_EXTRA_FILES)
|
||||||
|
ifeq (,$(BEFORE))
|
||||||
|
print-pretty-single-time-diff::
|
||||||
|
@echo 'Error: Usage: $(MAKE) print-pretty-single-time-diff AFTER=path/to/file.v.after-timing BEFORE=path/to/file.v.before-timing'
|
||||||
|
$(HIDE)false
|
||||||
|
else
|
||||||
|
ifeq (,$(AFTER))
|
||||||
|
print-pretty-single-time-diff::
|
||||||
|
@echo 'Error: Usage: $(MAKE) print-pretty-single-time-diff AFTER=path/to/file.v.after-timing BEFORE=path/to/file.v.before-timing'
|
||||||
|
$(HIDE)false
|
||||||
|
else
|
||||||
|
print-pretty-single-time-diff::
|
||||||
|
$(HIDE)$(COQMAKE_BOTH_SINGLE_TIMING_FILES) --fuzz=$(TIMING_FUZZ) --sort-by=$(TIMING_SORT_BY) $(TIMING_USER_ARG) $(AFTER) $(BEFORE) $(TIME_OF_PRETTY_BUILD_FILE) $(TIME_OF_PRETTY_BUILD_EXTRA_FILES)
|
||||||
|
endif
|
||||||
|
endif
|
||||||
|
pretty-timed:
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(PARENT)" make-pretty-timed
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" print-pretty-timed
|
||||||
|
.PHONY: pretty-timed make-pretty-timed make-pretty-timed-before make-pretty-timed-after print-pretty-timed print-pretty-timed-diff print-pretty-single-time-diff
|
||||||
|
|
||||||
|
# Extension points for actions to be performed before/after the all target
|
||||||
|
pre-all::
|
||||||
|
@# Extension point
|
||||||
|
$(HIDE)if [ "$(COQMAKEFILE_VERSION)" != "$(COQ_VERSION)" ]; then\
|
||||||
|
echo "W: This Makefile was generated by Coq $(COQMAKEFILE_VERSION)";\
|
||||||
|
echo "W: while the current Coq version is $(COQ_VERSION)";\
|
||||||
|
fi
|
||||||
|
.PHONY: pre-all
|
||||||
|
|
||||||
|
post-all::
|
||||||
|
@# Extension point
|
||||||
|
.PHONY: post-all
|
||||||
|
|
||||||
|
real-all: $(VOFILES) $(if $(USEBYTE),bytefiles,optfiles)
|
||||||
|
.PHONY: real-all
|
||||||
|
|
||||||
|
real-all.timing.diff: $(VOFILES:.vo=.v.timing.diff)
|
||||||
|
.PHONY: real-all.timing.diff
|
||||||
|
|
||||||
|
bytefiles: $(CMOFILES) $(CMAFILES)
|
||||||
|
.PHONY: bytefiles
|
||||||
|
|
||||||
|
optfiles: $(if $(DO_NATDYNLINK),$(CMXSFILES))
|
||||||
|
.PHONY: optfiles
|
||||||
|
|
||||||
|
# FIXME, see Ralf's bugreport
|
||||||
|
# quick is deprecated, now renamed vio
|
||||||
|
vio: $(VOFILES:.vo=.vio)
|
||||||
|
.PHONY: vio
|
||||||
|
quick: vio
|
||||||
|
$(warning "'make quick' is deprecated, use 'make vio' or consider using 'vos' files")
|
||||||
|
.PHONY: quick
|
||||||
|
|
||||||
|
vio2vo:
|
||||||
|
$(TIMER) $(COQC) $(COQDEBUG) $(COQFLAGS) $(COQLIBS) \
|
||||||
|
-schedule-vio2vo $(J) $(VOFILES:%.vo=%.vio)
|
||||||
|
.PHONY: vio2vo
|
||||||
|
|
||||||
|
# quick2vo is undocumented
|
||||||
|
quick2vo:
|
||||||
|
$(HIDE)make -j $(J) vio
|
||||||
|
$(HIDE)VIOFILES=$$(for vofile in $(VOFILES); do \
|
||||||
|
viofile="$$(echo "$$vofile" | sed "s/\.vo$$/.vio/")"; \
|
||||||
|
if [ "$$vofile" -ot "$$viofile" -o ! -e "$$vofile" ]; then printf "$$viofile "; fi; \
|
||||||
|
done); \
|
||||||
|
echo "VIO2VO: $$VIOFILES"; \
|
||||||
|
if [ -n "$$VIOFILES" ]; then \
|
||||||
|
$(TIMER) $(COQC) $(COQDEBUG) $(COQFLAGS) $(COQLIBS) -schedule-vio2vo $(J) $$VIOFILES; \
|
||||||
|
fi
|
||||||
|
.PHONY: quick2vo
|
||||||
|
|
||||||
|
checkproofs:
|
||||||
|
$(TIMER) $(COQC) $(COQDEBUG) $(COQFLAGS) $(COQLIBS) \
|
||||||
|
-schedule-vio-checking $(J) $(VOFILES:%.vo=%.vio)
|
||||||
|
.PHONY: checkproofs
|
||||||
|
|
||||||
|
vos: $(VOFILES:%.vo=%.vos)
|
||||||
|
.PHONY: vos
|
||||||
|
|
||||||
|
vok: $(VOFILES:%.vo=%.vok)
|
||||||
|
.PHONY: vok
|
||||||
|
|
||||||
|
validate: $(VOFILES)
|
||||||
|
$(TIMER) $(COQCHK) $(COQCHKFLAGS) $(COQLIBS_NOML) $^
|
||||||
|
.PHONY: validate
|
||||||
|
|
||||||
|
only: $(TGTS)
|
||||||
|
.PHONY: only
|
||||||
|
|
||||||
|
# Documentation targets #######################################################
|
||||||
|
|
||||||
|
html: $(GLOBFILES) $(VFILES)
|
||||||
|
$(SHOW)'COQDOC -d html $(GAL)'
|
||||||
|
$(HIDE)mkdir -p html
|
||||||
|
$(HIDE)$(COQDOC) \
|
||||||
|
-toc $(COQDOCFLAGS) -html $(GAL) $(COQDOCLIBS) -d html $(VFILES)
|
||||||
|
|
||||||
|
mlihtml: $(MLIFILES:.mli=.cmi)
|
||||||
|
$(SHOW)'CAMLDOC -d $@'
|
||||||
|
$(HIDE)mkdir $@ || rm -rf $@/*
|
||||||
|
$(HIDE)$(CAMLDOC) -html \
|
||||||
|
-d $@ -m A $(CAMLDEBUG) $(CAMLDOCFLAGS) $(MLIFILES) $(FINDLIBPKGS)
|
||||||
|
|
||||||
|
all-mli.tex: $(MLIFILES:.mli=.cmi)
|
||||||
|
$(SHOW)'CAMLDOC -latex $@'
|
||||||
|
$(HIDE)$(CAMLDOC) -latex \
|
||||||
|
-o $@ -m A $(CAMLDEBUG) $(CAMLDOCFLAGS) $(MLIFILES) $(FINDLIBPKGS)
|
||||||
|
|
||||||
|
all.ps: $(VFILES)
|
||||||
|
$(SHOW)'COQDOC -ps $(GAL)'
|
||||||
|
$(HIDE)$(COQDOC) \
|
||||||
|
-toc $(COQDOCFLAGS) -ps $(GAL) $(COQDOCLIBS) \
|
||||||
|
-o $@ `$(COQDEP) -sort $(VFILES)`
|
||||||
|
|
||||||
|
all.pdf: $(VFILES)
|
||||||
|
$(SHOW)'COQDOC -pdf $(GAL)'
|
||||||
|
$(HIDE)$(COQDOC) \
|
||||||
|
-toc $(COQDOCFLAGS) -pdf $(GAL) $(COQDOCLIBS) \
|
||||||
|
-o $@ `$(COQDEP) -sort $(VFILES)`
|
||||||
|
|
||||||
|
# FIXME: not quite right, since the output name is different
|
||||||
|
gallinahtml: GAL=-g
|
||||||
|
gallinahtml: html
|
||||||
|
|
||||||
|
all-gal.ps: GAL=-g
|
||||||
|
all-gal.ps: all.ps
|
||||||
|
|
||||||
|
all-gal.pdf: GAL=-g
|
||||||
|
all-gal.pdf: all.pdf
|
||||||
|
|
||||||
|
# ?
|
||||||
|
beautify: $(BEAUTYFILES)
|
||||||
|
for file in $^; do mv $${file%.beautified} $${file%beautified}old && mv $${file} $${file%.beautified}; done
|
||||||
|
@echo 'Do not do "make clean" until you are sure that everything went well!'
|
||||||
|
@echo 'If there were a problem, execute "for file in $$(find . -name \*.v.old -print); do mv $${file} $${file%.old}; done" in your shell/'
|
||||||
|
.PHONY: beautify
|
||||||
|
|
||||||
|
# Installation targets ########################################################
|
||||||
|
#
|
||||||
|
# There rules can be extended in Makefile.local
|
||||||
|
# Extensions can't assume when they run.
|
||||||
|
|
||||||
|
# We use $(file) to avoid generating a very long command string to pass to the shell
|
||||||
|
# (cf https://coq.zulipchat.com/#narrow/stream/250632-Coq-Platform-devs-.26-users/topic/Strange.20command.20length.20limit.20on.20Linux)
|
||||||
|
# However Apple ships old make which doesn't have $(file) so we need a fallback
|
||||||
|
$(file >.hasfile,1)
|
||||||
|
HASFILE:=$(shell if [ -e .hasfile ]; then echo 1; rm .hasfile; fi)
|
||||||
|
|
||||||
|
MKFILESTOINSTALL= $(if $(HASFILE),$(file >.filestoinstall,$(FILESTOINSTALL)),\
|
||||||
|
$(shell rm -f .filestoinstall) \
|
||||||
|
$(foreach x,$(FILESTOINSTALL),$(shell printf '%s\n' "$x" >> .filestoinstall)))
|
||||||
|
|
||||||
|
# findlib needs the package to not be installed, so we remove it before
|
||||||
|
# installing it (see the call to findlib_remove)
|
||||||
|
install: META
|
||||||
|
@$(MKFILESTOINSTALL)
|
||||||
|
$(HIDE)code=0; for f in $$(cat .filestoinstall); do\
|
||||||
|
if ! [ -f "$$f" ]; then >&2 echo $$f does not exist; code=1; fi \
|
||||||
|
done; exit $$code
|
||||||
|
$(HIDE)for f in $$(cat .filestoinstall); do\
|
||||||
|
df="`$(COQMKFILE) -destination-of "$$f" $(COQLIBS)`";\
|
||||||
|
if [ "$$?" != "0" -o -z "$$df" ]; then\
|
||||||
|
echo SKIP "$$f" since it has no logical path;\
|
||||||
|
else\
|
||||||
|
install -d "$(COQLIBINSTALL)/$$df" &&\
|
||||||
|
install -m 0644 "$$f" "$(COQLIBINSTALL)/$$df" &&\
|
||||||
|
echo INSTALL "$$f" "$(COQLIBINSTALL)/$$df";\
|
||||||
|
fi;\
|
||||||
|
done
|
||||||
|
$(call findlib_remove)
|
||||||
|
$(call findlib_install, META $(FINDLIBFILESTOINSTALL))
|
||||||
|
$(HIDE)$(MAKE) install-extra -f "$(SELF)"
|
||||||
|
@rm -f .filestoinstall
|
||||||
|
install-extra::
|
||||||
|
@# Extension point
|
||||||
|
.PHONY: install install-extra
|
||||||
|
|
||||||
|
META: $(METAFILE)
|
||||||
|
$(HIDE)if [ "$(METAFILE)" ]; then \
|
||||||
|
cat "$(METAFILE)" | grep -v 'directory.*=.*' > META; \
|
||||||
|
fi
|
||||||
|
|
||||||
|
install-byte:
|
||||||
|
$(call findlib_install, $(CMAFILES) $(CMOFILESTOINSTALL), -add)
|
||||||
|
|
||||||
|
install-doc:: html mlihtml
|
||||||
|
@# Extension point
|
||||||
|
$(HIDE)install -d "$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/html"
|
||||||
|
$(HIDE)for i in html/*; do \
|
||||||
|
dest="$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/$$i";\
|
||||||
|
install -m 0644 "$$i" "$$dest";\
|
||||||
|
echo INSTALL "$$i" "$$dest";\
|
||||||
|
done
|
||||||
|
$(HIDE)install -d \
|
||||||
|
"$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/mlihtml"
|
||||||
|
$(HIDE)for i in mlihtml/*; do \
|
||||||
|
dest="$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/$$i";\
|
||||||
|
install -m 0644 "$$i" "$$dest";\
|
||||||
|
echo INSTALL "$$i" "$$dest";\
|
||||||
|
done
|
||||||
|
.PHONY: install-doc
|
||||||
|
|
||||||
|
uninstall::
|
||||||
|
@# Extension point
|
||||||
|
@$(MKFILESTOINSTALL)
|
||||||
|
$(call findlib_remove)
|
||||||
|
$(HIDE)for f in $$(cat .filestoinstall); do \
|
||||||
|
df="`$(COQMKFILE) -destination-of "$$f" $(COQLIBS)`" &&\
|
||||||
|
instf="$(COQLIBINSTALL)/$$df/`basename $$f`" &&\
|
||||||
|
rm -f "$$instf" &&\
|
||||||
|
echo RM "$$instf" ;\
|
||||||
|
done
|
||||||
|
$(HIDE)for f in $$(cat .filestoinstall); do \
|
||||||
|
df="`$(COQMKFILE) -destination-of "$$f" $(COQLIBS)`" &&\
|
||||||
|
echo RMDIR "$(COQLIBINSTALL)/$$df/" &&\
|
||||||
|
(rmdir "$(COQLIBINSTALL)/$$df/" 2>/dev/null || true); \
|
||||||
|
done
|
||||||
|
@rm -f .filestoinstall
|
||||||
|
|
||||||
|
.PHONY: uninstall
|
||||||
|
|
||||||
|
uninstall-doc::
|
||||||
|
@# Extension point
|
||||||
|
$(SHOW)'RM $(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/html'
|
||||||
|
$(HIDE)rm -rf "$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/html"
|
||||||
|
$(SHOW)'RM $(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/mlihtml'
|
||||||
|
$(HIDE)rm -rf "$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/mlihtml"
|
||||||
|
$(HIDE) rmdir "$(COQDOCINSTALL)/$(INSTALLCOQDOCROOT)/" || true
|
||||||
|
.PHONY: uninstall-doc
|
||||||
|
|
||||||
|
# Cleaning ####################################################################
|
||||||
|
#
|
||||||
|
# There rules can be extended in Makefile.local
|
||||||
|
# Extensions can't assume when they run.
|
||||||
|
|
||||||
|
clean::
|
||||||
|
@# Extension point
|
||||||
|
$(SHOW)'CLEAN'
|
||||||
|
$(HIDE)rm -f $(CMOFILES)
|
||||||
|
$(HIDE)rm -f $(CMIFILES)
|
||||||
|
$(HIDE)rm -f $(CMAFILES)
|
||||||
|
$(HIDE)rm -f $(CMXFILES)
|
||||||
|
$(HIDE)rm -f $(CMXAFILES)
|
||||||
|
$(HIDE)rm -f $(CMXSFILES)
|
||||||
|
$(HIDE)rm -f $(OFILES)
|
||||||
|
$(HIDE)rm -f $(CMXAFILES:.cmxa=.a)
|
||||||
|
$(HIDE)rm -f $(MLGFILES:.mlg=.ml)
|
||||||
|
$(HIDE)rm -f $(CMXFILES:.cmx=.cmt)
|
||||||
|
$(HIDE)rm -f $(MLIFILES:.mli=.cmti)
|
||||||
|
$(HIDE)rm -f $(ALLDFILES)
|
||||||
|
$(HIDE)rm -f $(NATIVEFILES)
|
||||||
|
$(HIDE)find . -name .coq-native -type d -empty -delete
|
||||||
|
$(HIDE)rm -f $(VOFILES)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.vio)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.vos)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.vok)
|
||||||
|
$(HIDE)rm -f $(BEAUTYFILES) $(VFILES:=.old)
|
||||||
|
$(HIDE)rm -f all.ps all-gal.ps all.pdf all-gal.pdf all.glob all-mli.tex
|
||||||
|
$(HIDE)rm -f $(VFILES:.v=.glob)
|
||||||
|
$(HIDE)rm -f $(VFILES:.v=.tex)
|
||||||
|
$(HIDE)rm -f $(VFILES:.v=.g.tex)
|
||||||
|
$(HIDE)rm -f pretty-timed-success.ok
|
||||||
|
$(HIDE)rm -f META
|
||||||
|
$(HIDE)rm -rf html mlihtml
|
||||||
|
.PHONY: clean
|
||||||
|
|
||||||
|
cleanall:: clean
|
||||||
|
@# Extension point
|
||||||
|
$(SHOW)'CLEAN *.aux *.timing'
|
||||||
|
$(HIDE)rm -f $(foreach f,$(VFILES:.v=),$(dir $(f)).$(notdir $(f)).aux)
|
||||||
|
$(HIDE)rm -f $(TIME_OF_BUILD_FILE) $(TIME_OF_BUILD_BEFORE_FILE) $(TIME_OF_BUILD_AFTER_FILE) $(TIME_OF_PRETTY_BUILD_FILE) $(TIME_OF_PRETTY_BOTH_BUILD_FILE)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.v.timing)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.v.before-timing)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.v.after-timing)
|
||||||
|
$(HIDE)rm -f $(VOFILES:.vo=.v.timing.diff)
|
||||||
|
$(HIDE)rm -f .lia.cache .nia.cache
|
||||||
|
.PHONY: cleanall
|
||||||
|
|
||||||
|
archclean::
|
||||||
|
@# Extension point
|
||||||
|
$(SHOW)'CLEAN *.cmx *.o'
|
||||||
|
$(HIDE)rm -f $(NATIVEFILES)
|
||||||
|
$(HIDE)rm -f $(CMOFILES:%.cmo=%.cmx)
|
||||||
|
.PHONY: archclean
|
||||||
|
|
||||||
|
|
||||||
|
# Compilation rules ###########################################################
|
||||||
|
|
||||||
|
$(MLIFILES:.mli=.cmi): %.cmi: %.mli
|
||||||
|
$(SHOW)'CAMLC -c $<'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLC) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) $<
|
||||||
|
|
||||||
|
$(MLGFILES:.mlg=.ml): %.ml: %.mlg
|
||||||
|
$(SHOW)'COQPP $<'
|
||||||
|
$(HIDE)$(COQPP) $<
|
||||||
|
|
||||||
|
# Stupid hack around a deficient syntax: we cannot concatenate two expansions
|
||||||
|
$(filter %.cmo, $(MLFILES:.ml=.cmo) $(MLGFILES:.mlg=.cmo)): %.cmo: %.ml
|
||||||
|
$(SHOW)'CAMLC -c $<'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLC) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) $<
|
||||||
|
|
||||||
|
# Same hack
|
||||||
|
$(filter %.cmx, $(MLFILES:.ml=.cmx) $(MLGFILES:.mlg=.cmx)): %.cmx: %.ml
|
||||||
|
$(SHOW)'CAMLOPT -c $(FOR_PACK) $<'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTC) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) $(FOR_PACK) $<
|
||||||
|
|
||||||
|
|
||||||
|
$(MLLIBFILES:.mllib=.cmxs): %.cmxs: %.cmxa
|
||||||
|
$(SHOW)'CAMLOPT -shared -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) \
|
||||||
|
-shared -o $@ $<
|
||||||
|
|
||||||
|
$(MLLIBFILES:.mllib=.cma): %.cma: | %.mllib
|
||||||
|
$(SHOW)'CAMLC -a -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) -a -o $@ $^
|
||||||
|
|
||||||
|
$(MLLIBFILES:.mllib=.cmxa): %.cmxa: | %.mllib
|
||||||
|
$(SHOW)'CAMLOPT -a -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) -a -o $@ $^
|
||||||
|
|
||||||
|
|
||||||
|
$(MLPACKFILES:.mlpack=.cmxs): %.cmxs: %.cmxa
|
||||||
|
$(SHOW)'CAMLOPT -shared -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) \
|
||||||
|
-shared -o $@ $<
|
||||||
|
|
||||||
|
$(MLPACKFILES:.mlpack=.cmxa): %.cmxa: %.cmx | %.mlpack
|
||||||
|
$(SHOW)'CAMLOPT -a -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) -a -o $@ $<
|
||||||
|
|
||||||
|
$(MLPACKFILES:.mlpack=.cma): %.cma: %.cmo | %.mlpack
|
||||||
|
$(SHOW)'CAMLC -a -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) -a -o $@ $^
|
||||||
|
|
||||||
|
$(MLPACKFILES:.mlpack=.cmo): %.cmo: | %.mlpack
|
||||||
|
$(SHOW)'CAMLC -pack -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) -pack -o $@ $^
|
||||||
|
|
||||||
|
$(MLPACKFILES:.mlpack=.cmx): %.cmx: | %.mlpack
|
||||||
|
$(SHOW)'CAMLOPT -pack -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) -pack -o $@ $^
|
||||||
|
|
||||||
|
# This rule is for _CoqProject with no .mllib nor .mlpack
|
||||||
|
$(filter-out $(MLLIBFILES:.mllib=.cmxs) $(MLPACKFILES:.mlpack=.cmxs) $(addsuffix .cmxs,$(PACKEDFILES)) $(addsuffix .cmxs,$(LIBEDFILES)),$(MLFILES:.ml=.cmxs) $(MLGFILES:.mlg=.cmxs)): %.cmxs: %.cmx
|
||||||
|
$(SHOW)'[deprecated,use-mllib-or-mlpack] CAMLOPT -shared -o $@'
|
||||||
|
$(HIDE)$(TIMER) $(CAMLOPTLINK) $(CAMLDEBUG) $(CAMLFLAGS) $(FINDLIBPKGS) \
|
||||||
|
-shared -o $@ $<
|
||||||
|
|
||||||
|
# can't make
|
||||||
|
# https://www.gnu.org/software/make/manual/make.html#Static-Pattern
|
||||||
|
# work with multiple target rules
|
||||||
|
# so use eval in a loop instead
|
||||||
|
# with grouped targets https://www.gnu.org/software/make/manual/make.html#Multiple-Targets
|
||||||
|
# if available (GNU Make >= 4.3)
|
||||||
|
ifneq (,$(filter grouped-target,$(.FEATURES)))
|
||||||
|
define globvorule=
|
||||||
|
|
||||||
|
# take care to $$ variables using $< etc
|
||||||
|
$(1).vo $(1).glob &: $(1).v | $$(VDFILE)
|
||||||
|
$$(SHOW)COQC $(1).v
|
||||||
|
$$(HIDE)$$(TIMER) $$(COQC) $$(COQDEBUG) $$(TIMING_ARG) $$(PROFILE_ARG) $$(COQFLAGS) $$(COQLIBS) $(1).v
|
||||||
|
$$(HIDE)$$(PROFILE_ZIP)
|
||||||
|
ifeq ($(COQDONATIVE), "yes")
|
||||||
|
$$(SHOW)COQNATIVE $(1).vo
|
||||||
|
$$(HIDE)$$(call TIMER,$(1).vo.native) $$(COQNATIVE) $$(COQLIBS) $(1).vo
|
||||||
|
endif
|
||||||
|
|
||||||
|
endef
|
||||||
|
else
|
||||||
|
|
||||||
|
$(VOFILES): %.vo: %.v | $(VDFILE)
|
||||||
|
$(SHOW)COQC $<
|
||||||
|
$(HIDE)$(TIMER) $(COQC) $(COQDEBUG) $(TIMING_ARG) $(PROFILE_ARG) $(COQFLAGS) $(COQLIBS) $<
|
||||||
|
$(HIDE)$(PROFILE_ZIP)
|
||||||
|
ifeq ($(COQDONATIVE), "yes")
|
||||||
|
$(SHOW)COQNATIVE $@
|
||||||
|
$(HIDE)$(call TIMER,$@.native) $(COQNATIVE) $(COQLIBS) $@
|
||||||
|
endif
|
||||||
|
|
||||||
|
# this is broken :( todo fix if we ever find a solution that doesn't need grouped targets
|
||||||
|
$(GLOBFILES): %.glob: %.v
|
||||||
|
$(SHOW)'COQC $< (for .glob)'
|
||||||
|
$(HIDE)$(TIMER) $(COQC) $(COQDEBUG) $(COQFLAGS) $(COQLIBS) $<
|
||||||
|
|
||||||
|
endif
|
||||||
|
|
||||||
|
$(foreach vfile,$(VFILES:.v=),$(eval $(call globvorule,$(vfile))))
|
||||||
|
|
||||||
|
$(VFILES:.v=.vio): %.vio: %.v
|
||||||
|
$(SHOW)COQC -vio $<
|
||||||
|
$(HIDE)$(TIMER) $(COQC) -vio $(COQDEBUG) $(COQFLAGS) $(COQLIBS) $<
|
||||||
|
|
||||||
|
$(VFILES:.v=.vos): %.vos: %.v
|
||||||
|
$(SHOW)COQC -vos $<
|
||||||
|
$(HIDE)$(TIMER) $(COQC) -vos $(COQDEBUG) $(COQFLAGS) $(COQLIBS) $<
|
||||||
|
|
||||||
|
$(VFILES:.v=.vok): %.vok: %.v
|
||||||
|
$(SHOW)COQC -vok $<
|
||||||
|
$(HIDE)$(TIMER) $(COQC) -vok $(COQDEBUG) $(COQFLAGS) $(COQLIBS) $<
|
||||||
|
|
||||||
|
$(addsuffix .timing.diff,$(VFILES)): %.timing.diff : %.before-timing %.after-timing
|
||||||
|
$(SHOW)PYTHON TIMING-DIFF $*.{before,after}-timing
|
||||||
|
$(HIDE)$(MAKE) --no-print-directory -f "$(SELF)" print-pretty-single-time-diff BEFORE=$*.before-timing AFTER=$*.after-timing TIME_OF_PRETTY_BUILD_FILE="$@"
|
||||||
|
|
||||||
|
$(BEAUTYFILES): %.v.beautified: %.v
|
||||||
|
$(SHOW)'BEAUTIFY $<'
|
||||||
|
$(HIDE)$(TIMER) $(COQC) $(COQDEBUG) $(COQFLAGS) $(COQLIBS) -beautify $<
|
||||||
|
|
||||||
|
$(TEXFILES): %.tex: %.v
|
||||||
|
$(SHOW)'COQDOC -latex $<'
|
||||||
|
$(HIDE)$(COQDOC) $(COQDOCFLAGS) -latex $< -o $@
|
||||||
|
|
||||||
|
$(GTEXFILES): %.g.tex: %.v
|
||||||
|
$(SHOW)'COQDOC -latex -g $<'
|
||||||
|
$(HIDE)$(COQDOC) $(COQDOCFLAGS) -latex -g $< -o $@
|
||||||
|
|
||||||
|
$(HTMLFILES): %.html: %.v %.glob
|
||||||
|
$(SHOW)'COQDOC -html $<'
|
||||||
|
$(HIDE)$(COQDOC) $(COQDOCFLAGS) -html $< -o $@
|
||||||
|
|
||||||
|
$(GHTMLFILES): %.g.html: %.v %.glob
|
||||||
|
$(SHOW)'COQDOC -html -g $<'
|
||||||
|
$(HIDE)$(COQDOC) $(COQDOCFLAGS) -html -g $< -o $@
|
||||||
|
|
||||||
|
# Dependency files ############################################################
|
||||||
|
|
||||||
|
ifndef MAKECMDGOALS
|
||||||
|
-include $(ALLDFILES)
|
||||||
|
else
|
||||||
|
ifneq ($(filter-out archclean clean cleanall printenv make-pretty-timed make-pretty-timed-before make-pretty-timed-after print-pretty-timed print-pretty-timed-diff print-pretty-single-time-diff,$(MAKECMDGOALS)),)
|
||||||
|
-include $(ALLDFILES)
|
||||||
|
endif
|
||||||
|
endif
|
||||||
|
|
||||||
|
.SECONDARY: $(ALLDFILES)
|
||||||
|
|
||||||
|
redir_if_ok = > "$@" || ( RV=$$?; rm -f "$@"; exit $$RV )
|
||||||
|
|
||||||
|
GENMLFILES:=$(MLGFILES:.mlg=.ml)
|
||||||
|
$(addsuffix .d,$(ALLSRCFILES)): $(GENMLFILES)
|
||||||
|
|
||||||
|
$(addsuffix .d,$(MLIFILES)): %.mli.d: %.mli
|
||||||
|
$(SHOW)'CAMLDEP $<'
|
||||||
|
$(HIDE)$(CAMLDEP) $(OCAMLLIBS) "$<" $(redir_if_ok)
|
||||||
|
|
||||||
|
$(addsuffix .d,$(MLGFILES)): %.mlg.d: %.ml
|
||||||
|
$(SHOW)'CAMLDEP $<'
|
||||||
|
$(HIDE)$(CAMLDEP) $(OCAMLLIBS) "$<" $(redir_if_ok)
|
||||||
|
|
||||||
|
$(addsuffix .d,$(MLFILES)): %.ml.d: %.ml
|
||||||
|
$(SHOW)'CAMLDEP $<'
|
||||||
|
$(HIDE)$(CAMLDEP) $(OCAMLLIBS) "$<" $(redir_if_ok)
|
||||||
|
|
||||||
|
$(addsuffix .d,$(MLLIBFILES)): %.mllib.d: %.mllib
|
||||||
|
$(SHOW)'OCAMLLIBDEP $<'
|
||||||
|
$(HIDE)$(OCAMLLIBDEP) -c $(OCAMLLIBS) "$<" $(redir_if_ok)
|
||||||
|
|
||||||
|
$(addsuffix .d,$(MLPACKFILES)): %.mlpack.d: %.mlpack
|
||||||
|
$(SHOW)'OCAMLLIBDEP $<'
|
||||||
|
$(HIDE)$(OCAMLLIBDEP) -c $(OCAMLLIBS) "$<" $(redir_if_ok)
|
||||||
|
|
||||||
|
# If this makefile is created using a _CoqProject we have coqdep get
|
||||||
|
# options from it. This avoids argument length limits for pathological
|
||||||
|
# projects. Note that extra options might be on the command line.
|
||||||
|
VDFILE_FLAGS:=$(if _CoqProject,-f _CoqProject,) $(CMDLINE_COQLIBS) $(CMDLINE_VFILES)
|
||||||
|
|
||||||
|
$(VDFILE): _CoqProject $(VFILES)
|
||||||
|
$(SHOW)'COQDEP VFILES'
|
||||||
|
$(HIDE)$(COQDEP) $(if $(strip $(METAFILE)),-m "$(METAFILE)") -vos -dyndep var $(VDFILE_FLAGS) $(redir_if_ok)
|
||||||
|
|
||||||
|
# Misc ########################################################################
|
||||||
|
|
||||||
|
byte:
|
||||||
|
$(HIDE)$(MAKE) all "OPT:=-byte" -f "$(SELF)"
|
||||||
|
.PHONY: byte
|
||||||
|
|
||||||
|
opt:
|
||||||
|
$(HIDE)$(MAKE) all "OPT:=-opt" -f "$(SELF)"
|
||||||
|
.PHONY: opt
|
||||||
|
|
||||||
|
# This is deprecated. To extend this makefile use
|
||||||
|
# extension points and Makefile.local
|
||||||
|
printenv::
|
||||||
|
$(warning printenv is deprecated)
|
||||||
|
$(warning write extensions in Makefile.local or include Makefile.conf)
|
||||||
|
@echo 'COQLIB = $(COQLIB)'
|
||||||
|
@echo 'COQCORELIB = $(COQCORELIB)'
|
||||||
|
@echo 'DOCDIR = $(DOCDIR)'
|
||||||
|
@echo 'OCAMLFIND = $(OCAMLFIND)'
|
||||||
|
@echo 'HASNATDYNLINK = $(HASNATDYNLINK)'
|
||||||
|
@echo 'SRC_SUBDIRS = $(SRC_SUBDIRS)'
|
||||||
|
@echo 'COQ_SRC_SUBDIRS = $(COQ_SRC_SUBDIRS)'
|
||||||
|
@echo 'COQCORE_SRC_SUBDIRS = $(COQCORE_SRC_SUBDIRS)'
|
||||||
|
@echo 'OCAMLFIND = $(OCAMLFIND)'
|
||||||
|
@echo 'PP = $(PP)'
|
||||||
|
@echo 'COQFLAGS = $(COQFLAGS)'
|
||||||
|
@echo 'COQLIB = $(COQLIBS)'
|
||||||
|
@echo 'COQLIBINSTALL = $(COQLIBINSTALL)'
|
||||||
|
@echo 'COQDOCINSTALL = $(COQDOCINSTALL)'
|
||||||
|
.PHONY: printenv
|
||||||
|
|
||||||
|
# Generate a .merlin file. If you need to append directives to this
|
||||||
|
# file you can extend the merlin-hook target in Makefile.local
|
||||||
|
.merlin:
|
||||||
|
$(SHOW)'FILL .merlin'
|
||||||
|
$(HIDE)echo 'FLG $(COQMF_CAMLFLAGS)' > .merlin
|
||||||
|
$(HIDE)echo 'B $(COQCORELIB)' >> .merlin
|
||||||
|
$(HIDE)echo 'S $(COQCORELIB)' >> .merlin
|
||||||
|
$(HIDE)$(foreach d,$(COQCORE_SRC_SUBDIRS), \
|
||||||
|
echo 'B $(COQCORELIB)$(d)' >> .merlin;)
|
||||||
|
$(HIDE)$(foreach d,$(COQ_SRC_SUBDIRS), \
|
||||||
|
echo 'S $(COQLIB)$(d)' >> .merlin;)
|
||||||
|
$(HIDE)$(foreach d,$(SRC_SUBDIRS), echo 'B $(d)' >> .merlin;)
|
||||||
|
$(HIDE)$(foreach d,$(SRC_SUBDIRS), echo 'S $(d)' >> .merlin;)
|
||||||
|
$(HIDE)$(MAKE) merlin-hook -f "$(SELF)"
|
||||||
|
.PHONY: merlin
|
||||||
|
|
||||||
|
merlin-hook::
|
||||||
|
@# Extension point
|
||||||
|
.PHONY: merlin-hook
|
||||||
|
|
||||||
|
# prints all variables
|
||||||
|
debug:
|
||||||
|
$(foreach v,\
|
||||||
|
$(sort $(filter-out $(INITIAL_VARS) INITIAL_VARS,\
|
||||||
|
$(.VARIABLES))),\
|
||||||
|
$(info $(v) = $($(v))))
|
||||||
|
.PHONY: debug
|
||||||
|
|
||||||
|
.DEFAULT_GOAL := all
|
||||||
|
|
||||||
|
# Users can create Makefile.local-late to hook into double-colon rules
|
||||||
|
# or add other needed Makefile code, using defined
|
||||||
|
# variables if necessary.
|
||||||
|
-include Makefile.local-late
|
||||||
|
|
||||||
|
# Local Variables:
|
||||||
|
# mode: makefile-gmake
|
||||||
|
# End:
|
||||||
71
share/popl08-tutorial-Fsub/Makefile.conf
Normal file
|
|
@ -0,0 +1,71 @@
|
||||||
|
# This configuration file was generated by running:
|
||||||
|
# coq_makefile -f _CoqProject -o Makefile
|
||||||
|
|
||||||
|
COQBIN?=
|
||||||
|
ifneq (,$(COQBIN))
|
||||||
|
# add an ending /
|
||||||
|
COQBIN:=$(COQBIN)/
|
||||||
|
endif
|
||||||
|
COQMKFILE ?= "$(COQBIN)coq_makefile"
|
||||||
|
|
||||||
|
###############################################################################
|
||||||
|
# #
|
||||||
|
# Project files. #
|
||||||
|
# #
|
||||||
|
###############################################################################
|
||||||
|
|
||||||
|
COQMF_CMDLINE_VFILES :=
|
||||||
|
COQMF_SOURCES := $(shell $(COQMKFILE) -sources-of -f _CoqProject $(COQMF_CMDLINE_VFILES))
|
||||||
|
COQMF_VFILES := $(filter %.v, $(COQMF_SOURCES))
|
||||||
|
COQMF_MLIFILES := $(filter %.mli, $(COQMF_SOURCES))
|
||||||
|
COQMF_MLFILES := $(filter %.ml, $(COQMF_SOURCES))
|
||||||
|
COQMF_MLGFILES := $(filter %.mlg, $(COQMF_SOURCES))
|
||||||
|
COQMF_MLPACKFILES := $(filter %.mlpack, $(COQMF_SOURCES))
|
||||||
|
COQMF_MLLIBFILES := $(filter %.mllib, $(COQMF_SOURCES))
|
||||||
|
COQMF_METAFILE =
|
||||||
|
|
||||||
|
###############################################################################
|
||||||
|
# #
|
||||||
|
# Path directives (-I, -R, -Q). #
|
||||||
|
# #
|
||||||
|
###############################################################################
|
||||||
|
|
||||||
|
COQMF_OCAMLLIBS =
|
||||||
|
COQMF_SRC_SUBDIRS =
|
||||||
|
COQMF_COQLIBS = -R . Fsub
|
||||||
|
COQMF_COQLIBS_NOML = -R . Fsub
|
||||||
|
COQMF_CMDLINE_COQLIBS =
|
||||||
|
|
||||||
|
###############################################################################
|
||||||
|
# #
|
||||||
|
# Coq configuration. #
|
||||||
|
# #
|
||||||
|
###############################################################################
|
||||||
|
|
||||||
|
COQMF_COQLIB=/usr/lib/coq/
|
||||||
|
COQMF_COQCORELIB=/usr/lib/coq/../coq-core/
|
||||||
|
COQMF_DOCDIR=/usr/share/doc/
|
||||||
|
COQMF_OCAMLFIND=/usr/bin/ocamlfind
|
||||||
|
COQMF_CAMLFLAGS=-thread -bin-annot -strict-sequence -w -a+1..3-4+5..8-9+10..26-27+28..39-40-41-42+43-44-45+46..47-48+49..57-58+59..66-67-68+69-70
|
||||||
|
COQMF_WARN=-warn-error +a-3
|
||||||
|
COQMF_HASNATDYNLINK=true
|
||||||
|
COQMF_COQ_SRC_SUBDIRS=boot config lib clib kernel library engine pretyping interp gramlib parsing proofs tactics toplevel printing ide stm vernac plugins/btauto plugins/cc plugins/derive plugins/extraction plugins/firstorder plugins/funind plugins/ltac plugins/ltac2 plugins/micromega plugins/nsatz plugins/ring plugins/rtauto plugins/ssr plugins/ssrmatching plugins/syntax
|
||||||
|
COQMF_COQ_NATIVE_COMPILER_DEFAULT=no
|
||||||
|
COQMF_WINDRIVE=
|
||||||
|
|
||||||
|
###############################################################################
|
||||||
|
# #
|
||||||
|
# Native compiler. #
|
||||||
|
# #
|
||||||
|
###############################################################################
|
||||||
|
|
||||||
|
COQMF_COQPROJECTNATIVEFLAG =
|
||||||
|
|
||||||
|
###############################################################################
|
||||||
|
# #
|
||||||
|
# Extra variables. #
|
||||||
|
# #
|
||||||
|
###############################################################################
|
||||||
|
|
||||||
|
COQMF_OTHERFLAGS =
|
||||||
|
COQMF_INSTALLCOQDOCROOT = Fsub
|
||||||